Any integer
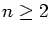
can be written in a unique way as the product of
its powerful part and its squarefree part, that is, as
n=
mr where
m is a powerful number and
r a squarefree number, with gcd(
m,
r)=1. We
denote these two parts of an integer
n by
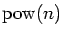
and
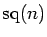
respectively, setting for convenience
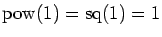
.
We first
examine the behavior of the counting functions
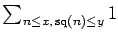
and
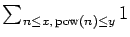
.
Letting
P(
n) stand for the largest prime factor of
n, we then provide asymptotic values of
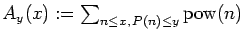
and
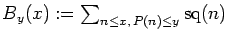
when
y=
x1/u with
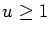
fixed. We also examine the size of
Ay(
x) and
By(
x) when
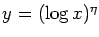
for some
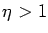
.
Finally, we prove that
Ay(
x) will coincide with
By(
x) in the
sense that
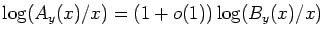
as
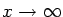
if we choose
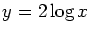
.

