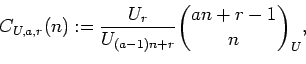For all integers
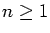
we define the generalized Lucasnomial
Fuss-Catalan numbers
and
prove their integrality. Here
U is a fundamental Lucas sequence,
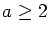
and
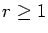
are integers, and
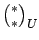
denotes a
Lucasnomial coefficient. If
U =
I,
where
In =
n, then the
CI,a,r(
n) are the usual generalized Fuss-Catalan numbers. With the
assumption that
U is regular, we show that
U(a-1)n+k divides
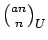
for all
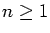
but a set of asymptotic density 0 if
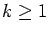
,
but only for a small set if

.
This small set is
finite when
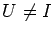
and at most of upper asymptotic density
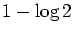
when
U =
I. We also determine
all triples (
U,
a,
k), where
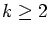
,
for which the
exceptional set of density 0 is actually finite, and in fact empty.