Асеев В. В.
Отображения, мало изменяющие фиксированное ангармоническое отношение
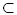
Для заданного комплексного числа λ ≠ 0, 1 рассматриваются локальные гомеоморфизмы области D   , которые в окрестности каждой точки мало (с заданным параметром малости δ) меняют ангармоническое отношение тетрад с фиксированным ангармоническим отношением λ. Доказывается квазиконформность таких отображений и выводятся оценки коэффициента квазиконформности, стремящиеся к 1 при δ → 0.
|
Aseev V. V.
Mappings slightly changing a fixed cross-ratio
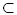
Given a complex number λ ≠ 0, 1, we consider local homeomorphisms of a domain D that, in a neighborhood of every point, change slightly (with a given smallness parameter δ) the cross-ratio of tetrads with fixed cross-ratio λ. We prove the quasiconformality of these mappings and obtain bounds for the coefficient of quasiconformality tending to 1 as δ → 0.
|
