| |
|
|
| |
Volume 4, Issue 3, Article 56 |
|
|
|
|
|
| |
Separation and Disconjugacy
|
| |
|
Authors: |
Richard C. Brown, |
|
| |
|
Keywords:
|
Separation, Symmetric second order differential operator, Disconjugacy, Limit-point. |
|
| |
|
Date Received:
|
21/11/02 |
|
| |
|
Date Accepted:
|
25/03/03 |
|
| |
|
Subject Codes: |
26D10, 34C10,34L99, 47E05.
|
|
| |
|
Editors: |
A. M. Fink, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
We show that certain properties of positive solutions of disconjugate second order differential expressions ![$ M[y]=-(py^{prime})^{prime}+qy$](images/130_02_JIPAM/img1.gif) imply the separation of the minimal and maximal operators determined by imply the separation of the minimal and maximal operators determined by  in in 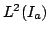 where where 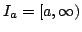 , ,  , i.e., the property that , i.e., the property that ![$ % M[y]in L^2(I_a)Rightarrow qyin L^2(I_a)$](images/130_02_JIPAM/img6.gif) . This result will allow the development of several new sufficient conditions for separation and various inequalities associated with separation. Some of these allow for rapidly oscillating . This result will allow the development of several new sufficient conditions for separation and various inequalities associated with separation. Some of these allow for rapidly oscillating 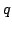 . It is shown in particular that expressions . It is shown in particular that expressions  with with  solutions are separated, a property leading to a new proof and generalization of a 1971 separation criterion due to Everitt and Giertz. A final result shows that the disconjugacy of solutions are separated, a property leading to a new proof and generalization of a 1971 separation criterion due to Everitt and Giertz. A final result shows that the disconjugacy of 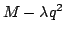 for some for some 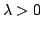 implies the separation of implies the separation of  . .
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



