| |
|
|
| |
Volume 5, Issue 1, Article 18 |
|
|
|
|
|
| |
Asymptotic Behavior Of The Approximation Numbers Of The Hardy-Type Operator From $L^p$ Into $L^q$
|
| |
|
Authors: |
J. Lang, O. Mendez, A. Nekvinda, |
|
| |
|
Keywords:
|
Approximation numbers, Hardy operator, Voltera operator. |
|
| |
|
Date Received:
|
17/12/03 |
|
| |
|
Date Accepted:
|
04/02/04 |
|
| |
|
Subject Codes: |
Primary 46E30; Secondary 47B38
|
|
| |
|
Editors: |
Don B. Hinton, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
We consider the Hardy-type operator and establish properties of 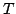 as a map from as a map from 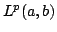 into into 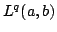 for for 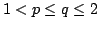 , , 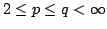 and and 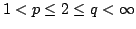 . The main result is that, with appropriate assumptions on . The main result is that, with appropriate assumptions on  and and 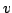 , the approximation numbers , the approximation numbers 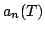 of of 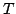 satisfy the inequality satisfy the inequality when 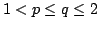 or or 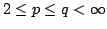 , and in the case , and in the case 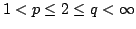 we have and where we have and where  and constants and constants 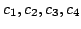 . Upper and lower estimates for the . Upper and lower estimates for the  and and  norms of norms of 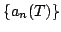 are also given. are also given.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



