| |
|
|
| |
Volume 5, Issue 4, Article 105 |
|
|
|
|
|
| |
On Embedding of the Class $H^{\omega }$
|
| |
|
Authors: |
Laszlo Leindler, |
|
| |
|
Keywords:
|
Embedding relation, Bounded variation, Continuity. |
|
| |
|
Date Received:
|
24/08/04 |
|
| |
|
Date Accepted:
|
29/09/04 |
|
| |
|
Subject Codes: |
26A15, 26A21, 26A45.
|
|
| |
|
Editors: |
Hüseyin Bor, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In [4] we extended an interesting theorem of Medvedeva [5] pertaining to the embedding relation 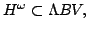 where where 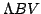 denotes the set of functions of denotes the set of functions of 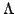 -bounded variation, which is encountered in the theory of Fourier trigonometric series. Now we give a further generalization of our result. Our new theorem tries to unify the notion of -bounded variation, which is encountered in the theory of Fourier trigonometric series. Now we give a further generalization of our result. Our new theorem tries to unify the notion of  -variation due to Young [6], and that of the generalized Wiener class -variation due to Young [6], and that of the generalized Wiener class 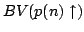 due to Kita and Yoneda [3]. For further references we refer to the paper by Goginava [2]. due to Kita and Yoneda [3]. For further references we refer to the paper by Goginava [2].
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



