| |
|
|
| |
Volume 7, Issue 1, Article 16 |
|
|
|
|
|
| |
Inequalities Involving a Logarithmically Convex Function and Their Applications to Special Functions
|
| |
|
Authors: |
Edward Neuman, |
|
| |
|
Keywords:
|
Logarithmically convex functions, inequalities, gamma function, Riemann's zeta function, complete elliptic integrals of the first kind. |
|
| |
|
Date Received:
|
29/10/05 |
|
| |
|
Date Accepted:
|
09/11/05 |
|
| |
|
Subject Codes: |
Pri: 26D07, 26D20. Sec: 33B15, 11M06, 33
|
|
| |
|
Editors: |
Themistocles M. Rassias, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
It has been shown that if  is a differentiable, logarithmically convex function on nonnegative semi-axis, then the function is a differentiable, logarithmically convex function on nonnegative semi-axis, then the function ![$ [f(x)]^a/f(ax)$](images/324_05_JIPAM/img2.gif) , ( , (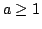 ) is decreasing on its domain. Applications to inequalities involving gamma function, Riemann's zeta function, and the complete elliptic integrals of the first kind are included. ) is decreasing on its domain. Applications to inequalities involving gamma function, Riemann's zeta function, and the complete elliptic integrals of the first kind are included.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



