JIPAM

Hyers-Ulam-Rassias Stability of the $K$-Quadratic Functional Equation  
 
  Authors: Mohamed Ait Sibaha, Belaid Bouikhalene, Elhoucien Elqorachi,  
  Keywords: Group, Additive equation, Quadratic equation, Hyers-Ulam-Rassias stability.  
  Date Received: 26/01/07  
  Date Accepted: 08/06/07  
  Subject Codes:

39B82, 39B52, 39B32.

  
  Editors: Kazimierz Nikodem,  
 
  Abstract:

In this paper we obtain the Hyers-Ulam-Rassias stability for the functional equation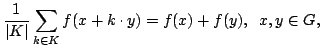

$displaystyle frac{1}{vert Kvert}sum_{kin K}f(x+kcdot y)=f(x)+f(y),;;x,yin G, $
where $ K$ is a finite cyclic transformation group of the abelian group $ (G,+) $, acting by automorphisms of $ G$. As a consequence we can derive the Hyers-Ulam-Rassias stability of the quadratic and the additive functional equations. ;


This article was printed from JIPAM
http://jipam.vu.edu.au

The URL for this article is:
http://jipam.vu.edu.au/article.php?sid=902