
| The Geometer's Angle no. 1: Marriages of Incommensuables |
|---|
The last construction to present in this issue's column involves a marriage between a simple harmonic sequence that is converted into the square root rectangle progression. I have never seen this construction anywhere, and I invite readers to let me know if they have, and to also invite some of the mathematical readership to offer a proof for why this construction is mathematically sound.
As part of the preview to the procedure, I include the Rule of Thales. It states that in a semicircle, any point on the circumference, when drawn to the ends of the diameter, will be a 90° angle. It was this rule, and the simple fact that a square can be inscribed within the boundary of a circle using two diameters that intersect at 90° that led me to discovering this marriage.
This construction is rich in quality of content. Along with the harmonic progression and the square root square rectangle sequence, it also contains the diagonal / reciprocal relationship as well as two geometric progressions. Whenever we have the diagonal / reciprocal relationship, we also have the "occult center", so called because it is "hidden from the eye".
Lastly, the construction also demonstrates the "geometric
mean between two extremes". As defined: when a semicircle
is drawn, and the diameter is divided into any two measures -
the two
extremes - the perpendicular to this diameter, at the junction
of these two measures, will yield the geometric mean between
the two extremes.
PROCEDURE
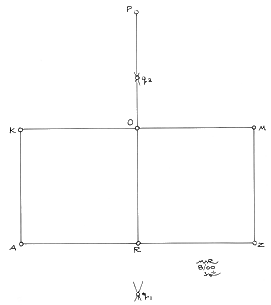
1. As in Figure 2.1, draw any rectangle, AKMZ, and bisect it (as in, RP, by q1 and q2), to obtain the midpoint, O. For this construction, I have chosen the double square for purely aesthetic reasons. What is of importance is the midpoint, O, as it will be converted to a diameter of a circle.
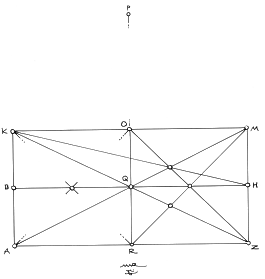
2. Figure 2.2 illustrates the development of the armature, or the grid, of any rectangle. The grid is started by drawing the two diagonals, AM and KZ, and the half-diagonals, KH, RM, and, ZO. Please note that a rectangle has eight half-diagonals, as the lines come from the four corners, and go to two adjacent sides. This simple foundation leads to a fairly rich and complex system of development. For our purposes, we will only need the three half-diagonals mentioned.
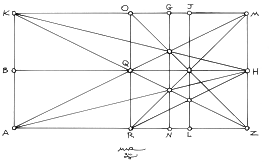
3. In Figure 2.2a, the grid is further developed in order to find the fractional parts of the rectangle, AKMZ. A rule for the development of a grid within the rectangle is that where a diagonal and a half-diagonal intersect (which I call an "eye"), it will yield thirds of both the perimeter and area of a rectangle. This simple fact can yield complex systems, depending on the needs of the designer. NG is the caesura, or break, of one of the thirds horizontally, so that we have: NZ = 1/3, NA = 2/3, and ZA = 3/3 of the width of rectangle, AKMZ. Also shown is another aspect of the grid work, and it works as a simple arithmetic calculation: ½ x ½ = ¼. Where OZ, for example, crosses, BH, both being halves - ZO as a half-diagonal, and, BH, being a midline, yields a fourth. ZL is ¼ of ZA. As the intersection of the two diagonals, at Q, will generate the exact center of the rectangle, we now have the beginning of a harmonic progression: 1/1, ½, 1/3, and, ¼.
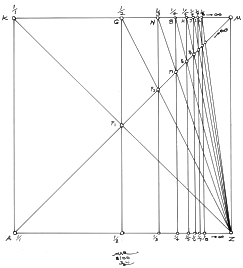
4. Next, in order to have more clarity on the development of this harmonic progression, see Figure 2.3. (I have selected a square for the demonstration, but again, this procedure applies to all rectangles.) By starting with the two diagonals, AM and ZK, and the half-diagonal, ZG, we can begin the harmonic progression: 1/1, ½, 1/3, ¼, 1/5, 1/6, 1/7, 1/8, …, 1/n, 1/n + 1… Z is the radiating point for the progression, and it generates points, p1, p2, p3, p4, p5, etc. along the diagonal, AM, so that by drawing through each of these 'p' points along the diagonal, AM, we generate points, G, N, B, H, J, I, L, etc., along the side, KM. This harmonic progression is infinite, and bound only by the medium used in the rendering. Figure 2.3a, and Figure 2.3b show this technique applied to the rectangle with which we started.

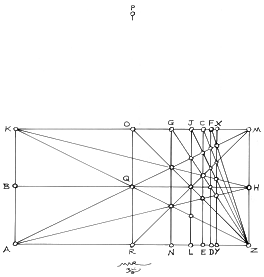
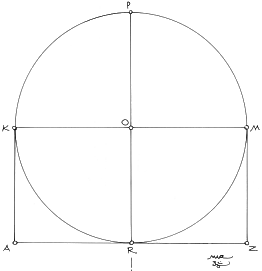
5. In Figure 2.4, a circle is drawn with center, O, and diameters, KM and RP. In Figure 2.1, KM was the side, KM, and the perpendicular, RP. Here, both have been converted into diameters. There are times in geometry where one element can become several things simultaneously. For our purposes, we will concentrate on the semicircle, KPM, and that the diameter, KM, that was a side of the original rectangle, and that now, it will also become the diagonal of all of the square root rectangles in the sequence. KM is a constant.
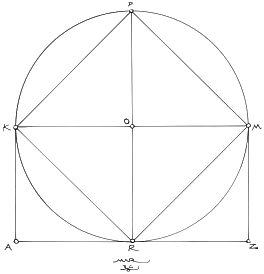
6. Figure 2.5 shows square, RKPR, inscribed within the circle. This simple fact holds the key to the marriage. It is vital to recognize that point, O, is ½ of KM. We now have a rectangle with side = 1, the Ö1 rectangle. Thus begins the sequence of the root rectangles. The Rule of Thales can be seen here four times, at R, K, P, and M, as a semicircle can begin and end at any of the infinite points of the circumference, and the application of any of the infinite number of diameters within the circle. In the sequence of the 'root' rectangles, the number under the radical sign will progress arithmetically, from 1 to infinity, with the Ö2 coming next, the Ö3 to follow, ad infinitum. In addition to this, one of the most outstanding qualities of the construction is this principle: the number of the denominator in the fractional harmonic progression below is always 1 more than the number under the radical sign in the sq rt sequence above! So, we have, ½ = Ö1, 1/3 = Ö2, ¼ = Ö3…, etc. A complex and beautiful marriage indeed!
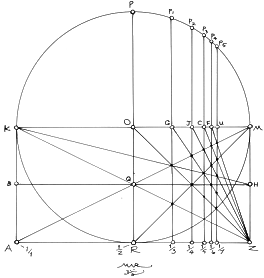
7. As the harmonic sequence of the rectangle is developed, as shown in Figure 2.6, the measures of ½, 1/3, ¼, and so on, are drawn up to intersect the circle at, p, p1, p2, p3, p4, etc. These 'p' points will become 90° angles for the root rectangle system.
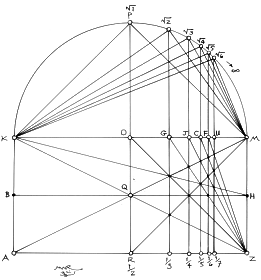
8. Figure 2.7 demonstrates the Rule of Thales along the semicircle, KPM. The 'p' points have been replaced by the radical signs of the beginning of the root rectangle sequence, which is also infinite. The harmonic progression is shown at the bottom of the rectangle, along, AZ. Remember that, KM, the diameter/diagonal length, is the constant, and it serves to render the fractional parts and the diagonal constant for the rectangles. Also, as noted in the introduction to this construction, GÖ2 (as an example) is the geometric mean between the two extremes, MG, and, GK; and as we will see in the next step, the points, G, J, C, and so on, become occult centers in the root rectangles.
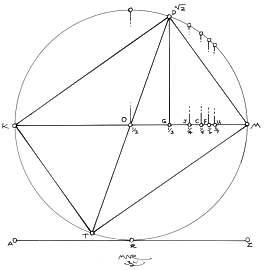
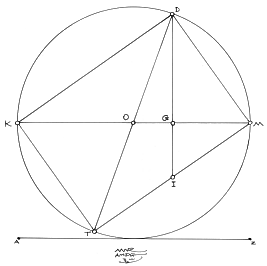
9. In Figure 2.8, the Ö2 rectangle, TKDT, has been isolated from the series for clarity's sake. Point T, has been generated by drawing the second diagonal, DT, by passing through the center, O, in what may be roughly termed glide reflection. Glide reflection is a type of symmetry operation where a point, a shape, an image has been reflected as in bilateral symmetry, but that it has also been rotated or flipped over to the opposite side of the axis, KM. This technique of drawing the second diagonal of each rectangle through O has been used to obtain all of the root rectangles, as seen in Figure 2.10. Figure 2.9 shows the Ö2 rectangle, TKDM, once again. In this part of the construction, the geometric mean, GD, has been extended to point I, to become the reciprocal, DI. GI, GM, GD, and GK are in a geometric progression, and are equal to the ratio of the rectangle, in this instance, 1: Ö2.
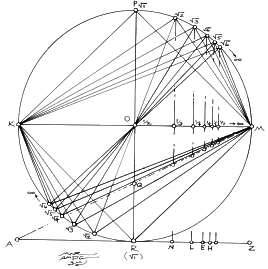
There may be other qualities to all of these relationships that I have overlooked, and the readership may want to bring them to my attention. As always, I welcome any information that will expand the rich substance of geometric relationships, and to share that knowledge with everyone. In the Geometer's Angle, I want to deepen our understanding of geometry, and to broaden our vision of the potential that lay beneath the surface of what geometry shows us. And although I mention and use some of the rules and propositions of Pythagoras, Euclid and other classical geometers, I also want to demonstrate another marriage: that of the creative mind with the power and the possibilities that geometry possesses.
