| |
|
Abstract: |
This article is concerned with the infimum 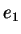 of the spectrum of the Schrödinger operator of the spectrum of the Schrödinger operator 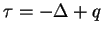 in in 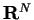 , ,  . It is assumed that . It is assumed that 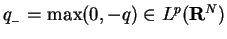 , where , where 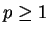 if if 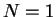 , ,  if if 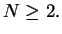 The infimum The infimum 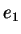 is estimated in terms of the is estimated in terms of the 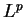 -norm of -norm of 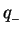 and the infimum and the infimum 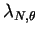 of a functional of a functional 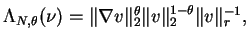 with with  element of the Sobolev space element of the Sobolev space 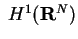 , where , where 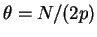 and and  . The result is optimal. The constant . The result is optimal. The constant 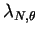 is known explicitly for is known explicitly for 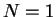 ; for ; for 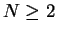 , it is estimated by the optimal constant , it is estimated by the optimal constant 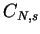 in the Sobolev inequality, where in the Sobolev inequality, where 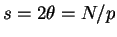 . A combination of these results gives an explicit lower bound for the infimum . A combination of these results gives an explicit lower bound for the infimum 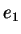 of the spectrum. The results improve and generalize those of Thirring [A Course in Mathematical Physics III. Quantum Mechanics of Atoms and Molecules, Springer, New York 1981] and Rosen [Phys. Rev. Lett., 49 (1982), 1885-1887] who considered the special case of the spectrum. The results improve and generalize those of Thirring [A Course in Mathematical Physics III. Quantum Mechanics of Atoms and Molecules, Springer, New York 1981] and Rosen [Phys. Rev. Lett., 49 (1982), 1885-1887] who considered the special case 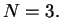 The infimum The infimum 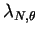 of the functional of the functional 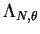 is calculated numerically (for is calculated numerically (for 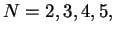 and and 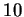 ) and compared with the lower bounds as found in this article. Also, the results are compared with these by Nasibov [Soviet. Math. Dokl., 40 (1990), 110-115]. ) and compared with the lower bounds as found in this article. Also, the results are compared with these by Nasibov [Soviet. Math. Dokl., 40 (1990), 110-115].
|



