| |
|
Abstract: |
Let 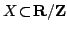 be a non-empty finite set and be a non-empty finite set and  be a real-valued function on be a real-valued function on ![$ [0,frac{1}{2}]$](images/118_05_JIPAM/img3.gif) . Let an energy of . Let an energy of 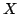 be the average value of be the average value of 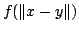 for for 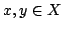 where where 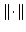 is the Euclidean distance on is the Euclidean distance on  . Let . Let 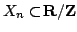 be an equally spaced be an equally spaced 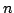 -point set. It is shown that if -point set. It is shown that if 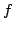 is monotone decreasing and convex, then among all is monotone decreasing and convex, then among all 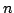 -point sets, the energy is minimized by -point sets, the energy is minimized by 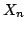 . Moreover, by giving a variant of a result of Bennett and Jameson, it is shown that if . Moreover, by giving a variant of a result of Bennett and Jameson, it is shown that if 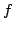 is convex, is convex, 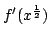 is concave and is concave and 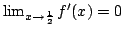 , then the energy of , then the energy of 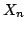 decreases with decreases with 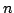 . .
|



