The three principal means most commonly held useful to architects and artists are the arithmetic, the geometric, and the harmonic means. The subject of the three means can be found both in ancient Greek sources and in crucial Renaissance architectural treatises such as those of Leon Battista Alberti and Andrea Palladio.[1]

As a very brief introduction to means, let me give a simplified definition and explanation of what a mean is. Mathematically, a mean is a quantity having a value intermediate between two other values, as determined by a specific formula or set of conditions. A mean is a number that stands in some proportionality (or other relationship) to a number lesser than it in value and another number greater than it in value. The outer two numbers are called extremes.[2] A mean is a kind of average between extremes, but the various types of means include averages that are more complex than the familiar concept of 'halfway in between' (i.e., the arithmetic mean).

The three means (B), with their formulae in terms of the extremes (A and C), are:

1. Arithmetic:

2. Geometric:

3. Arithmetic:

My main interests regarding means are in:

• the way that means can be employed compositionally within a frame;
• how means function in the development of organizational field grids;
• how means work to develop linear perspective and proportional grids;
• how the spiral can be generated from the geometric mean;
• how means can generate progressions, which is a development beyond their original function, leading to patterns and tessellations;
• the means' relationships to aural and visual components.

As an example, a mean can be used for the express purpose of composition, in the placement of a central or important element in a painter's canvas or an architect's plan or elevation. However, if desired, the idea of the mean can be extended beyond its original sense of a particular type of middle place or term to comprise a progression for the purposes of enlarging or reducing elements in an orderly mathematical fashion, and especially for purposes of visual perspective, the diminution of forms in pictorial space. Applying a mean to determine a progression is quite simple in the case of the arithmetic and geometric means, but in the case of the harmonic mean, it is not nearly as straightforward.

It was at this point that I approached Stephen R. Wassell, Associate Professor and Chair of the Mathematical Sciences Department at Sweet Briar College, Virginia, and Mathematics Editor of the Nexus Network Journal, with the question of how one could determine progressions based on the harmonic mean. His answer, "Arithmetic, Geometric and Harmonic Sequences", appears as an adjunct to this issue's Geometer's Angle column. [3] Steve and I share a common interest in the means. His paper does an excellent job in explaining the mathematics behind harmonic progressions, offering a general formula that, to our knowledge, does not exist in the literature.

Before we get to Steve's paper, let me exhibit how progressions can be used to generate perspective grids. In the six accompanying drawings on the geometric and harmonic progressions, we can see how a linear perspective grid system can be developed from either approach. The geometric progression used in Figure 1 is

Figure 1: Geometric progression within a square.

The harmonic progression used in Figure 2 is

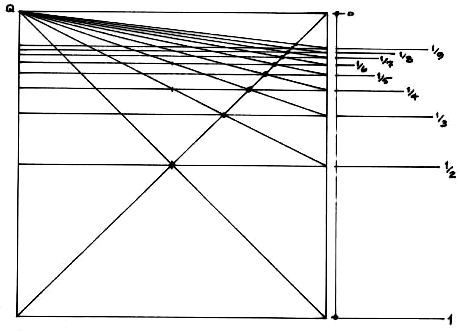Figure 2: Harmonic progression within a square.

Of the two, the eye sees that the harmonic progression is more naturalistic in portraying perspective space.

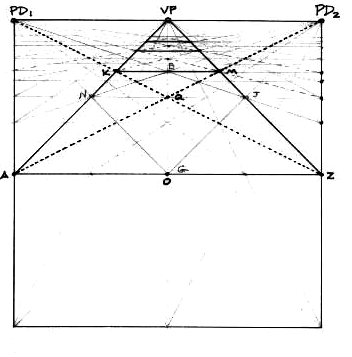Figure 3: "One-point" (parallel) perspective grid using harmonic and geometric progressions.

In Figure 3, guide lines for the diagonals of squares that run to the points of distance (PD₁ and PD₂) and use the harmonic progression in the square for their ordering have been drawn as dotted lines. AKMZ is a square in parallel perspective. AM and ZK are its diagonals, and GB and NJ are the square's midlines. Q is the center of the perspective square. Additional squares can be seen in the receding grid on the horizontal plane, and all orthogonals intersect at VP. The fronts and backs of all the squares remain parallel in one point perspective, and are called transversals.

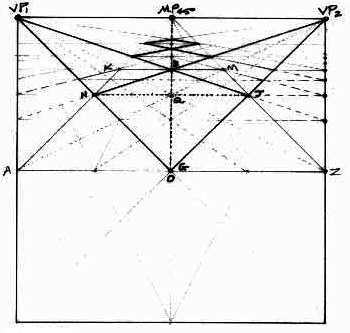Figure 4: "Two-point" (angular) perspective grid using geometric and harmonic progressions.

In Figure 4, the functions of the VPs and the PDs have reversed, as well as the sides and the diagonals of the squares in the horizontal plane. Now, GNBJ is the two-point square, and NJ and GB are diagonals. However, these components still rely on the harmonic progression for their diminution.

Figure 5

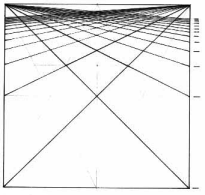Figure 6

In Figure 5 and Figure 6 both perspective grids are displayed as surfaces with the marks of the harmonic progression placed to the right of the squares.

Remember that these grids can be drawn in rectangles as well without any change to the appearance of the space.

My major interest in the information Steve provides is in researching the possibilities of finding geometric constructions that can demonstrate the mathematics of his paper. This can lead to new approaches in spatial rendering, as well as in fresh compositional endeavors, and even to tiling and tessellation patterns. My research may begin with Palladio's construction or one that I have developed, but my desire is to see if there is a geometric demonstration that can accompany the mathematical figures that Professor Wassell presents in this paper. I am uncertain of the specific relationships between music and the visual arts on this particular subject, but I plan to bring this up in discussions with those musical theorists who may be interested. There may be philosophical questions regarding these physical qualities of music and harmony that the mathematics may suggest for the artist and the architect to explore in the manipulation and composition of forms in physical materials. In other words, is there a correlation between the way we perceive space as symbolically represented in the perspective grids we invented in the Renaissance, and the musical ratios found in harmonic progressions? I will keep our readership updated on these developments.

NOTES
[1] The Greek mathematicians Nicomachus, Pappus, Iamblichus, and Theon of Smyrna all discuss the three principal means (along with 7 or so others) in their mathematical writings; cf. [Heath 1981: vol. 1, 85ff.] and [Nicomachus 1926: 281, note 3]. See [Alberti 1988: 308-309 (book 9, chapter 6)] and [Palladio 1997: 58-59 (book 1, chapter 23)] for Renaissance applications of the three means. For a brief overview of the rich history of means, see [Wassell 2002]. return to text

[2] One can generalize the concept of a mean to allow more than two "extreme" values, but this is unnecessary for the present discussion. return to text

[3] I would like to offer this kind of opportunity for collaboration to other associates who are working on projects similar to mine, or if there is a common subject that we have been discussing or debating, or whose work is of interest to me and our readership that pertains to things geometric, architectural, and artistic. return to text

REFERENCES
Alberti, Leon Battista. 1988. On the Art of Building in Ten Books. Joseph Rykwert, Neil Leach and Robert Tavernor, trans. Cambridge MA: MIT Press. To order this book from Amazon.com, click here.

Heath, Thomas L. 1981. A History of Greek Mathematics. 2 vols. 1921 rpt. New York: Dover Publications. To order this book from Amazon.com, click here.

Kappraff, Jay. 2000. The Arithmetic of Nicomachas of Gerasa and its Applications to Systems of Proportion. Pp.41-55 in Nexus Network Journal 2.

Nicomachus. 1926. Nicomachus of Gerasa: An Introduction to Arithmetic. Martin Luther D'Ooge, trans. New York: Macmillan.

Palladio, Andrea. 1997. The Four Books of Architecture. Robert Tavernor and Richard Schofield, trans. Cambridge MA: MIT Press.To order this book from Amazon.com, click here.

Wassell, Stephen R. 2002. Rediscovering a Family of Means. Forthcoming in The Mathematical Intelligencer 24.

Copyright ©2005 Kim Williams Books