APPLICATIONS OF A NEW PROPERTY OF CONICS IN ARCHITECTURE
In previous papers presented at ISAMA 99 [Martín-Zorraquino et al. 1999], the 9th International Congress of Graphic Engineering [Martín-Zorraquino et al. 1997]and Mathematics and Design 98 [Martín-Zorraquino et al. 1998], we set out by means of some interesting examples the applications of a new property of conics [Martín-Zorraquino et al. 1993] in architecture and in engineering. This paper sets forth the architectural possibilites that a new mathematical discovery allows us to achieve. First, the new property of conics has been proved, along with their two particular cases, further analysing a family of generated ellipses E(M) in such a way that by means of a simple law of linear arrangement, it is possible to generate the three-dimensional surface such that the sections perpendicular to the Z-axis are ellipses, proof of their ruled character. Next, we take as our example two alternative arrangements for Rio de Janeiro Metropolitan cathedral (Figure 1) [Brasil imágenes 1997], setting forth the interpenetration and parametrization techniques carried out in order to achieve these geometrical projects. In each arrangement a circular base is linked to a cross on the ridge above and parallel to the plane where the base circumference is located. These arrangements have the novel feature of the cross as an integral part of the construction, and the difference between the two possibilites depends on the style of cross choosen, that is, whether the Latin Immisa or the Greek cross is preferred. The three-dimensional development of the project has been achieved by the development of computer programs that have enabled us to depict the two arrangements in three-space, while working out an interesting method of parametrization of the final conic surface as a result of the process of interpenetration of two or more surfaces. Finally, we deal with aspects of construction both with concrete and metallic structures for the attainment of the geometric projects, such as, the original construction techniques for concrete shells used widely by Spanish arquitect Félix Candela in countries such as México, Colombia, United States and Spain.

MATHEMATICAL DEMOSTRATION OF THE NEW PROPERTY OF CONICS PARTICULARIZED TO THE ELLIPSE CASE
In the projects set out here as alternatives to the actual Rio de Janeiro Metropolitan Cathedral, we have made use of the new property of conics[Martin-Zorraquino et al, 1993] adapted to the particular case of the ellipse case. Hence, all the mathematical calculus needed for the graphic design of the projects are based on the expression that result from of the demonstration of the new property of conics for the case of the ellipse, as this philosophy of calculation can be extended, as is described below, to the other two remaining conics, namely, the hyperbola and the parabola.

Beginning then, with the demonstation of the new property of conics, let us first consider ellipse M (Figure 2), defined in the plane uv by the equation for the ellipse [see Appendix I]:

(1)

where a stands for the major semiaxis of the ellipse and b the minor semiaxis of the ellipse.

A straight line normal to ellipse M at point Q has been drawn, showing only a quarter of ellipse M as in Figure 2, from which the following property shall be demonstrated:

The loci of the points (x,y) mirrors of points (u,v) Î M, through the mapping stated in this figure (k Î Â), is in its turn another ellipse M' . The exception point V (apex of M) together with its image point V' (apex of M'), yields to:

(2)

where the value b²/a corresponds to the curvature radius at point V(a,0), being represented in the figure by the distance from point C1 to V(a,0). In the family E(M) of ellipses generated for the values k Î Â, there are two circumferences and two straight lines (ellipses with a null semiaxis).

In order to prove this property of the ellipse, which is common to all three conics, as further demonstrated, let us get at first, the slope of the straight line n normal to the generator ellipse M at point Q(u,v).

Deriving the equation (1) it yields:

(3)

Hence, the slope of the straight line normal to the tangent straight line Q(u,v) is yielded through the condition of perpendicularity between the two straight lines: m m' = -1.

Thus, it results that m'= -1/m, and therefore:

(4)

is the slope being sought.
Due to the similarities between triangles,

(5)

(but the reader should note that

and beware).

Again referring to Figure 2, making the calculation,

yields:

(5)

and since Q ¹ V (v ¹ 0), it brings about:

By substituting the previous expressions of u,v into equation (1), eventually it turns out the following points loci Q'(x,y):

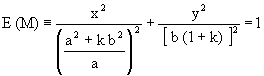(6)

This represents the Cartesian equation of an ellipse for all k Î Â, and by depending on the parameter k, it constitutes the equation of a family of ellipses E(M), generated from the generator ellipse M defined according to the equation (1).

ANALYSIS OF THE ELLIPSE FAMILY E(M)
In the ellipse family E(M) generated from the generator ellipse M defined according to equation (1), there are two circumferences and two straight lines. This is further demonstrated in Figure 3, where such particular cases have only been represented in one quarter of the two-dimension representation.

• Identifying the semiaxis of E(M), we have,

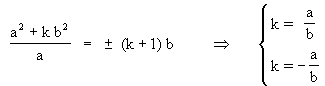Substituting those values into equation (6) gives rise respectively to the circumferences:

• In the same way, making each one of the semiaxes equal to zero yields:

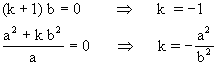The equality k= -1 gives rise to a symmetrical and horizontal segment, the center of which matches point O (the origin of the coordinates), having C1 (Figure 3 and Figure 4) as one of its edges.

With k= -a²/b², we have a symmetrical and vertical segment with its center point O, with C4 being one of its edges.

It can be easily proven that | a - b²/a | y | b - a²/b | are respectively the semilengths of such segments, noting the fact that the segment represents the distance between the centers of curvature in the horizontal axis; in the same way, the segment represents the distance between the centers of curvature in the vertical axis .

Figure 4 is a computer representation of different values of k, two straight lines, two circumferences and several ellipses, among which can be noticed the generator ellipse M of the family.

Every generated point and generated conic remains defined in their totality by a numerical parameter k referred to as 'the generator conic'. This constitutes a thoroughly exclusive property in comparison to any other known method of generating surfaces with conics.

In the process of generating conics of the family E(M), we can find semi-straight lines or straight lines (depending on whether the generator conic is an ellipse, a hyperbola or a parabola). Thus, a straight line can be dealt with mathematically and geometrically as a conic belonging to the family.

In the case of the generator ellipse, two circumferences are obtained that can be handled as conics within the family.

As a corollary, the following can be stated:

• A new concept appears: that of the "generator ellipse" or in general "generator conic" belonging to the corresponding family of generated conics
• It turns out that it is a novelty to handle the straight lines as ellipses with a null semi-axis .

GENERATION OF SURFACES FROM THE FAMILY E(M)
If it were possible to arrange in space, in a continuous way, this whole family of generated conics, we would obtain a surface having cross-sections that would also belong to the family.

This guideline for arranging the ellipses will be called the 'Arrangement Law' and shall correspond to a "generating line" upon which all transformed points coming from a single point of the generator ellipse shall rest. This means that each k applied to the generator ellipse will have its corresponding point upon the generating line in space. That is to say, each k applied to the generator ellipse will have its corresponding ellipse in space, which is an aditional arrangement condition for all parallel planes .

Each point belonging to the generator conic creates lines of the same family according to the 'Arrangement Law'. So, if this 'Arrangement Law' is a linear function of or proportional to the generating factor k, those lines shall be straight lines belonging to a ruled surface.

It is especially important to mention here in reference to matters of construction that those points belonging to the generating lines can be defined at once, by simply linking the homologous points between a straight line segment and a circumference. Thus a whole set of ellipses are obtained without the need to resort to traditional means for their generation.

The simplicity of this mathematical treatment deserves to be noted as a remarkable property, in comparison to the fact that usually the only simple treatment of similar ruled surfaces in science and technology is a graphic one. It is outstanding that, thanks to the 'Arrangement Law', an infinity of surfaces,whether be linear or not, can be settled up.

Substituting k for z in equation (6) according to the linear relation k=cz, for c = 1, we have:

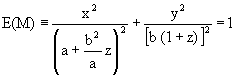(7)

which is the surface equation, whose cross-section curves are the ellipses of the family E(M), the z-coordinate being null in the generator ellipse plane, where all director curves or cross-section curves are located in planes parallel and perpendicular to the vertical axis Z.

Although the study of this surface with this equation was first undertaken with the aim of representing or characterizing the corresponding mathematical model (Figure 5), it has given rise to the ascertainment of remarkable properties and applications, especially in construction, owing largely to the fact that these surfaces are ruled ones, as shall be further demonstrated.

In Figure 5, k = z/c has been chosen according to the linear 'Arrangement Law'.

CONFIRMATION OF THE CONDITION OF RULED SURFACES
In order to prove this important characteristic of our surfaces defined according to equation (7), its cartesian equation shall have to be expressed through its parametric form:

(8)

as it is demonstrated in APPENDIX III.

Establishing the relation between the equation:

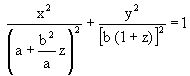
and the fundamental trigonometric form: sin² z + cos² z = 1

it is evident that:

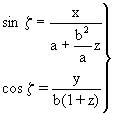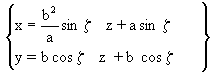(9)

and identifying the equations (8) and (9) it can be proved that the paramenter z can be easily removed to lead to equation (7), quod erat demostrandum.

AN EXAMPLE OF USING THE ARRANGEMENT LAW
As has been pointed out in the preceding section, depending on the relationship established between the parameter k that defines the set of cross-section curves belonging to the family of ellipses and the variable z, an infinity of surfaces will result. A special case of these surfaces occurs when the relationship between z and k is linear, resulting in a RULED SURFACE, as was demonstrated previously. This problem could be resolved by finding the equation for the ruled surface and its generating straight lines in order to develop a cover between a straight ridge and an elliptic base, given:

• Semimajor axis A and semiminor axis B of the elliptic base;
• Height H of the straight ridge;
• Length L of the straight ridge (parallel to A).

The general equation for all generated ellipses by the generator ellipse with semiaxis a and b will be as already stated, in accordance with equation (6):

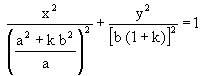(10)

In the particular case for the base:

(11)

(12)

For the straight ridge, the corresponding ellipse would have semiaxis L/2 and 0, for k= -1.

(13)

taking the center of the generator ellipse as the origin of the coordinates, and considering it located between the straight ridge and the base at a distance c below the straight ridge. The linear relation between "k" and "z" can be set forth by knowing that in the straight ridge z = c for k= -1, and in the generator ellipse z = 0 for k = 0,

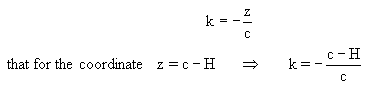(14)

From (11) and (13),

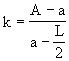(15)

From (12) and (15),

(16)

From (13) and (16),

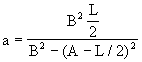(17)

From (14) and (15),

(18)

With values a, b and c the resulting equation for the surface f(x,y,z)=1 is:

(19)

(20)

All of what has been calculated above is shown in Figure 5.

In order to obtain the straight lines (generating lines according to the concept of ruled surfaces), it is sufficient to take several points on the generator ellipse and apply them the values k = -1 (straight ridge) and k = ko (base circumference). First, we shall have to obtain the equation of the normal straight line at the selected point of the generator ellipse. Second we shall have to draw the intersection between the normal straight line previously traced and the transformed ellipses (k= -1 and k = ko), obtaining in this way the coordinates x,y of the end of the straight line. The coordinate z stands for the distance with respect to the generator ellipse.

THE GEOMETRICAL AND MATHEMATICAL DEVELOPMENT OF THE ARCHITECTURAL PROJECT
The project of the alternative version of the Rio de Janeiro Cathedral in Brasil has been developed as an example of a direct application of this new property of conics to architecture with the particular requirement that the design shall include a cross at its straight ridge as an integral part of such a construction. Two patterns of crosses have been set out in this paper, the Latin Immisa cross and the Greek cross. The Greek cross is a cross with two arms of equal lenght that cross each other at right angles, the point of intersection of the arms being at their centerpoints. The Latin Immisa cross has arms of unequal lengths that cross each other at right angles, the point of intersection being, as in the Greek cross, at their centerpoints. This is different from the more common Latin cross, in which the arms are unequeal but which do not intersect at their middle point.

The fact that each cross is composed of two arms perpendicular between each other, disregarding the difference in their lengths, made us think about the intersection of two surfaces with straight ridges that were rotated by 90°. On the other hand, since the base to be linked to the straight ridge consists of a circumference (in this particular case, of an ellipse), the only possibility we have, judging by all that has been dealt with in the preceding sections, is the employment of the family of ellipses E(M) expressed by equation (6), which we repeat here:

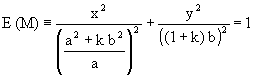(21)

Endowing the former expression with a linear 'Arrangement Law' of the form k = -z/c, where c represents the height between the ridge plane and the plane of the generator ellipse, we obtain the following expression both in Cartesian and parametric forms:

º

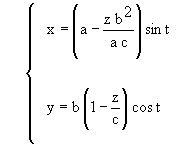(22)

where z and t are the two parameters of the previous expression, and the parameter z stands for the height of the cross-section curves with respect to the plane at height zero, or the plane where the generator ellipse is located. The parameter t stands for the angle formed by the vertical plane holding the generating line for a constant value of t with the vertical plane x = 0. A better exposition for the parametric representation of a surface is detailed in APPENDIX II.

As was mentioned before, a surface that links the straight ridge to the circular base will have to be obtained, and it can easily be seen that such a surface comes about as the result of extracting it from the general one (see the encircled detail of Figure 6), thus obtaining the elemental surface that will be used for the development of the cathedral project. To use our own terminology, from the general surface shown in Figure 6, called 'elemental surface 1', we will proceed to obtain the 'elemental surface 2', shown in Figure 7, by rotating the first surface by 90°.

The positioning of these figures is such that 'elemental surface 1' will correspond to the surface having both its major axis of the generator ellipse and its straight straight ridge parallel to the X axis. Therefore, both the major axis of the generator ellipse belonging to 'elemental surface 2' and its straight ridge are parallel to the Y axis.

From what has been discussed up to this point, the project will consist of the interpenetration between the two surfaces rotated 90° with respect to each other, or in other words, all the cross-section or director ellipses of the two elemental surfaces, cutting each other perpendicularly.

The following data is known:

• Radius R of the base circle;
• Height H between the ridge plane and the base one;
• Lengths L1 and L2 of the straight ridges of the elemental surfaces 1 and 2 respectively.

The equation from which we begin the further mathematical development of the project is given by equation (22) in its Cartesian form, where the linear relationship is given by k = -z/c, c being the distance between the generator ellipse located in the plane z = 0 (k = 0), and the straight ridge (k = -1).

The nex step consists of calculating the intersection between each pair of perpendicular director ellipses that are located in the same horizontal plane for every value of the parameter z, yielding the four intersection points as a solution of the equation system corresponding to the two elemental surfaces, in such a way that by achieving the same process for the whole set of the chosen values for the z parameter, and further joining the homologous intersection points, we arrive at the four intersection curves.

The intent of the preceding considerations is to build three point arrays, each one to store the coordinates (x, y, z) of the point sets belonging to the final surface, the rows of such arrays characterized by the t parameter and the columns characterized by the z parameter.

The quest for the values of the semiaxis a and b of the generator ellipse, and of the parameter c, in terms of the data that is known (i.e., R (base circle radius); H (height between the ridge plane and the base one); and L (length of the straight ridge), lead us to the results which were obtained in the previous section where we discussed how to deal with the 'Arrangement Law'.

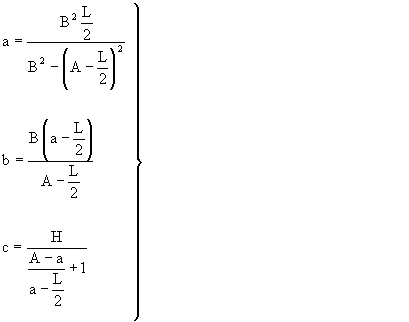(23)

The values A and B refer to the values of the semi-major and semi-minor axis of the ellipse (in this case, the radius of the base circle) located with respect to the plane of the straight ridge at a distance H, L being the length of the straight ridge.

The steps that follow consist of particularizing the aforementioned values of a, b and c for each of the two cathedral types in terms of the type of the cross chosen (Latin Immisa, with unequal and centered arms, or Greek, with equal and centered arms), along with the description of the process of interpenetration between elemental surfaces 1 and 2 in order to generate the eventual resultant surfaces for the designs. The project for each type of cross is illustrated.

PROJECT OF A CATHEDRAL BASED ON THE LATIN IMMISA CROSS
Defining the Latin Immisa cross as that with arms that are unequal and centered at a point located upon the vertical axis Z, we will designate as L1 the length of the minor arm of the cross parallel to the X axis and belonging to elemental surface 1. We will designate as L2 the length of the major arm of the cross parallel to the Y axis and belonging to elemental surface 2, in such a way that the values of the semiaxis and the relative locations of every one of the elemental surfaces will be determined according to the expressions (23).

The expression for elemental surface 1, that is, that with a minor arm that concurs with the direction of the X-axis, is deduced from equation (22) and will be given by:

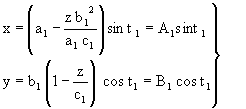(24)

The expression for elemental surface 2, that is, that whose major arm concurs with the direction of the Y-axi, is deduced from equation (22) by a rotation of 90°, and is given by:

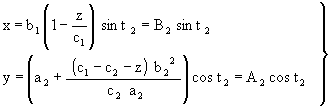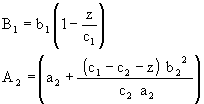(25)

Additionally, we want to take into account the following relationships:

(26)

where the values a₁, b₁, c₁ and a₂, b₂, c₂, for the elemental surfaces 1 and 2 respectively, are given by the following expressions obtained from (23) by simply making A=B=R and identifying L by L1 and L2 depending on the elemental surface to which it refers.

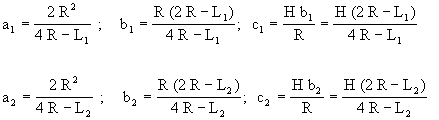(27)

It is interesting to mention as well, as it is proved by making the calculations that:

which justifies the fact that yields to B₁=B₂=B₀.

Eventually it can be verified that the sum of the semiaxis a₁ and b₁, as well as a₂ and b₂ from the generator ellipses correspond to the values of the radius R of the base circumference, which is a given.

We want to emphasize the fact that the generator ellipses of the elemental surfaces do not lie in the same plane (Figure 8), hence the mathematical expression for one of the two surfaces will have to be referred to in terms of the other. Therefore the values of the parameter z of the second surface have to be referred to with respect to the plane z = 0 of the generator ellipse of the first surface, according to z' = z-(c₁- c₂), a relationship that appears explicity in the value A₂.

When the system made up of equations (24) and (25) is resolved, the result yields the loci of the space points common to the two surfaces from which the eventual cathedral is formed, loci that will be also be the outcome of the process of interpenetration.

In consequence of what has been discussed above, the equations that define the nonplanar curves that result from the process of interpenetration for the case of Latin Immisa cross are given thus:

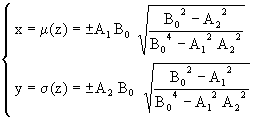(28)

The process of interpenetration consists, then, of first obtaining the four possible points of intersection generated by each of the ellipses belonging to elemental surfaces 1 and 2 situated on the same plane defined by parameter z. The next step is to eliminate the zones or stretches of the direction curves which are concealed (Figure 9 and Figure 10). This gives the utilizable encircling surface of the final resultant surface. The meeting of all homologous points of intersection will define the four intersecting curves between the two elemental surfaces (Figures 8, 9, 10).

For the next phase, the starting point will be the previous calculation process that consisted of selecting a determined number of direction curves that are common to the two surfaces of the cathedral, calculating their respective dimensions with reference to the plane containing the generating curve and which will be determined by parameter z. This will also supply the height of each direction plane with respect to the plane of the base circumference, the value of which is given by h = H-c+z. Then a suitable and sufficient number of generating straight lines is determined using parameter t, defined as the angle formed by the vertical plane which contains the direction straight line with the plane x = 0. Values of t in the direction of the Y axis towards the X axis are taken as positive, that is to say, clockwise in a Cartesian reference system.

The next step is to determine all the points at which each previously selected generating straight line cuts each and every one of the direction curves also selected in accordance with what was discussed in the paragraph above. Having obtained all the points of intersection, a point matrix is created for each of the x, y, z coordinates defined as [X], [Y] and [Z]. The columns for all the previous matrices will reflect the order number corresponding to the direction plane, beginning with the ridge plane and moving as far as the base plane. The rows, on the other hand, represent the order number of the generating straight lines beginning with the value t = 0 and finishing with t = 2p in a clockwise direction. Hence each place within the corresponding matrix defined by its row and column will correspond to the value of the x coordinate for the [X] matrix, y for [Y] and z for the corresponding [Z] matrix. From all the points obtained above, those which are inside the resultant surface will have to be disregarded using the process of interpenetration. It is advisable for the previously selected generators to include those which pass through the points of intersection of each pair of direction ellipses situated in the planes whose z parameter values were also selected.

From the point of view of construction, this cathedral project could be accomplished in two ways. One would involve the technique of reinforced concrete shells [Candela 1985; Faber 1970] for spans which are not too large, while the other would involve the use of metal structures for large spans. In either of these methods, one important feature is the absence of intermediate pillars, allowing completely open and diaphanous spaces. In those structures where the use of laminar reinforced concrete involves high building costs due in part to an excessive increase in thickness of the concrete layers, and where membrane stress calculations are no longer reliable for this type of structure, it is preferable to resort to metal structures involving the use of stronger, lighter and more resistant steel, making it possible to achieve spans of up to 300 metres without intermediate supports.

Having obtained the point matrices, according to the construction process using the technique of reinforced concrete laminar structures, the phase of erecting the wooden formwork would involve raising wooden piers of length h for each point Q(x,y,z) projected on the base circumference plane. The coordinates are stored in the corresponding matrices mentioned above, allowing the assembly of wooden strips or boards in pillar form. The ends of the pillars are subsequently joined, giving rise to the generating straight lines such that in certain sections of the cathedral they will go from the straight ridge to the base circumference, and in others from the straight ridge to the corresponding point on the curve of intersection, between the two surfaces, thereby forming the cathedral surface.

After the formwork, the necessary reinforcing bars are positioned and the concrete poured. Once the concrete has set, the formwork is removed, revealing a curved structure in the form of a concrete shell of a certain thickness capable of providing adequate rigidity and strength to withstand and absorb the stresses generated. The final surface will create a totally open interior space with no internal columns to take away light and space, one of the merits of this type of construction, devised by Spanish architect Félix Candela [Candela 1985; Faber 1970].

Designed with care, these surfaces would allow the creation of openings to accommodate rose windows, and other large apertures to let light enter. Glazing these openings with suitably coloured glass and engraving with appropriate religious images, in conjunction with the design of the top part of the space as a transparent cross, would project an extraordinary halo of light onto the altar into the interior of the cathedral.

The result of our cathedral project with the Latin Immisa cross is shown in Figure 11 and Figure 11a which took account the data R = 53 metres, H = 80 metres (which corresponds to the main dimensions of the Río de Janeiro cathedral), as well as the arms of the cross with values of L1 = 40 metres for the shorter, off-center, arm) and L2 = 50 metres for the longer arm, of "golden" proportions.

THE PROJECT FOR THE CATHEDRAL WITH A GREEK CROSS
The Greek cross is a particular case of the Latin Immisa cross where the arms have the same length equal to L. The corresponding expressions (27) now become the following ones:

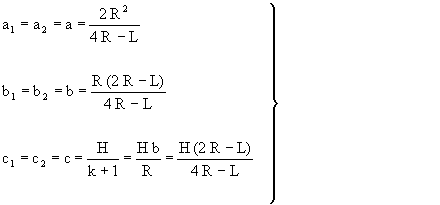(29)

It can be easily verified, as in the case of the Latin Immisa cross, that the sum of the semiaxis a and b of the generator ellipse corresponds to the radius R of the base circumference, which is a given.

In the discussion up to this point, we have worked out the values of a,b,c according to the equations of the previous case, since the Greek cross is a particular case of the Latin Immisa cross. The corresponding equations will be as follows. For the elemental surface 1, whose straight ridge lies parallel to the X axis, we have:

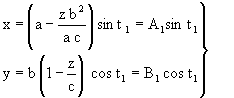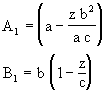(30)

For elemental surface 2, whose straight ridge lies parallel to the Y axis, and is rotated 90° with respect to elemental surface 1, we have:

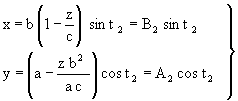(31)

In the previous expressions it can be observed that A₁=A₂=A₀ and B₁=B₂=B₀, these coeficients depending on the paramenter z. Thus the system formed with the four previous equations will lead to the loci of points belonging to the plane curves in accordance with the solution shown below (32), such that the intersection of such plane curves by whatever plane perpendicular to the Z axis gives rise to the four common points of the two ellipses located in the same cutting plane.

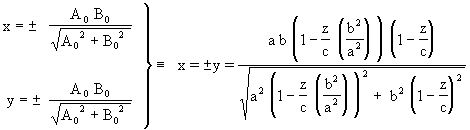(32)

In Figure 12, Figure 13 and Figure14 the process of interpenetration discussed in the previous sections is illustrated schematically for the project with the Greek cross instead of the Latin Immisa cross, showing the parallel planes of the base and of the straight ridge, between which the surface is formed, as well as the planes belonging to elemental surfaces 1 and 2. In this case the two generator ellipses lie in the same plane, since the arms of the cross are of the same length as well as the heights of c₁ and c₂ from each respective arm to the generator ellipse plane (z = 0). These figures also illustrate the four intersection points generated by the two generator ellipses, through which the four intersection curves pass, as result of the process of interpenetration between the two surfaces.

The final result of the Greek cross project is illustrated in Figure 15 and Figure 16, where the given parameters were R = 53 meters and H = 80 meters (both of which dimensions correspond to the main ones of the Metropolitan Cathedral of Río de Janeiro), together with the length of the arms of the cross L₁=L₂=30 meters.

THE ARCHITECTURAL CONCLUSION
In addition to the high level of originality of these design projects from a structural and mathematical point of view, demonstrated in the fact that the light generated in the ridge plane is an integral part while the straight ridge itself forms the roof and support, the symbolic religious character suggested by these surfaces is unquestionable and worthy of note. This religious character is expressed by the way the upper level in the form of a cross seems to embrace the whole space enclosed by the surface of the cathedral developed here, thus aspiring to join together the upper, divine, level with the lower, terrestrial, ones.

Click here to go to Appendix I, Appendix II and Appendix III.

REFERENCES
Brasil, imágenes. Publication of the Embassy of Brasil in Bogotá, Colombia. Cuaderno Nº 28, Pág. 29 (April 1997).

Candela, Félix. 1985. En defensa del formalismo y otros escritos. Bilbao: Ediciones Xarait.

Faber, Colin. 1970. Las estructuras de Candela. CECSA, Mexico.

Granero-Rodríguez, Francisco. 1985. Álgebra y geometría analítica. Madrid and Mexico City: McGraw-Hill.

Martín-Zorraquino, J.V, Francisco Granero-Rodríguez, José Luis Cano-Martín, J.J. Doria-Iriarte, J.J. 1999. "A Novel Version of the Cathedral Inspired in the Already Built one in Rio de Janeiro". Pp. 357-364 in ISAMA 99. Nathaniel Friedman and Javier Barallo, eds. Proceedings of the International Society of the Arts, Mathematics and Architecture (ISAMA) 99 conference, 7-11 June 1999, San Sebastián.

Martín-Zorraquino, J.V.. Francisco Granero-Rodríguez, J.J.Doria-Iriarte, J.J. 1997. "Otras Aportaciones y Resultados sobre la Nueva Familia de Figuras Geométricas Elementales con Cónicas". 9º International Congress of Graphic Engineering. Bilbao - S. Sebastián: UPV-EHU.

Martín-Zorraquino, J.V., Francisco Granero-Rodríguez, J.J. Doria-Iriarte. 1998. "New Properties of Conic Sections and the Ruled Surfaces Deriving from them. Selected Applications in Architecture and Engineering". Pp. 431-438 in Mathematics & Design 98. J. Barrallo, ed. Proceedings of the Second International Conference of Mathematics & Design 98. Sebastián: UPV-EHU.

Martín-Zorraquino, J.V., Francisco Granero-Rodríguez, J.J. Doria-Iriarte. 1993."Superficies Tridimensionales de Secciones Cónicas". Patent number P9301662/1993.

ABOUT THE AUTHORS
Prof. Dr. Martín Zorraquino is industrial engineer and Professor in Thermic Engineering at the High Technical School of Engineering in Bilbao (Spain) holding his professor's chair since 1966. He is director of the Heat Engines Department at the same university since 1987. During the last years, he has run ten research projects financed by the Basque Country University and the Basque Government itself. He has written several research articles.

Dr. Granero Rodriguez is industrial engineer and Lecturer in Applied Mathematics at the High Technical School of Engineering in Bilbao. He has written several research workings and several books on mathematics, five of them published by the publishing house McGraw-Hill.

Dr. Cano Martín is industrial engineer. He works as an engineer for a large firm located in the Basque Country.

Copyright ©2001 Kim Williams