
| Rosettes and Other Arrangements of Circles |
|---|
Department of Computer Science
Cardiff University
UK
INTRODUCTION
The process of design in art and architecture
generally involves the combination and manipulation of a relatively
small number of geometric elements to create both the underlying
structures as well as the overlaid decorative details. In this
paper we concentrate on patterns created by copies of just a
single geometric form - the circle. The circle is an extremely
significant shape. By virtue of its simplicity and its topology
it has been highly esteemed by many different cultures for millennia,
symbolising God, unity, perfection, eternity, stability, etc.
For instance, Ralph Waldo Emerson considered the circle to be
"the highest emblem in the cipher of the world" [Emerson
1920].
CIRCULAR ROSETTES
Circular rosettes have a long history,
going back at least 6000 years, and were popular for instance
in the Egyptian, Babylonian, Assyrian, and Greek cultures [Goodyear
1891]. Examples of some of the attractive arrangements of intersecting
circles at the Temple of Osiris (e.g. the so-called Flower and
Seed of Life) are given in Rawles comprehensive book [Rawles
1997]. Later, the rosette was a popular decorative pattern for
floors in Roman architecture [Schmelzeisen 1992]. A more modern
phenomena are the increased sightings of crop circles. Disregarding
the issue of the authenticity of their extraterrestrial origin,
it is worth noting that many involve intersecting circles forming
rosette-like patterns. In fact, circular rosettes appear in many
unexpected areas, from manholes [Melnick 1994] to Leonardo da
Vinci's knot patterns to clock faces to garden hedges (Figure 1).
A circular rosette is formed by taking copies of a circle and rotating them about a point—the rosette's centre (Figure 2). If the radius r of the circle is equal to the distance d between the point of rotation and the circle centres then the circles all meet at the centre of the rosette (Figure 3a). If the circle radii are smaller than d then they do not reach the rosette centre, creating a hole (Figure 3b). Likewise, an apparent hole is created when the circle radii are greater than d, although in this case the rosette centre is contained in all the circles. We see also that as the number of circles used to generate the rosettes increases the envelope of the external perimeter of the rosette converges to a circle with radius r+d while the envelope of the inner circle is a circle with radius d. Thus, we have the curious aspect that the same sized inner circular hole is created for a fixed value v, irrespective of whether r=d+v or r=d-v.
To simplify matters we shall only consider the first case in which the circles meet at the rosette centre. The points of intersection between the circles is given by

where t is the angle increment between successive circles,
i.e. if N number of circles then ![]() ,
and n is the intersection level such that 1 indicates
the intersection closest to the rosette's periphery, 2 the next
level closer in to the rosette's centre, and so on. This enables
us to verify some properties that suggest themselves on visual
inspection of the rosettes. First, with the exception of the
innermost and outermost regions of the rosette the interstices
formed by the overlapping circles form a sort of curvilinear
rhombus (Figure 9). Not
only do all the sides of these interstices have equal length,
but all the interstices have equal length sides. Second, there
are
,
and n is the intersection level such that 1 indicates
the intersection closest to the rosette's periphery, 2 the next
level closer in to the rosette's centre, and so on. This enables
us to verify some properties that suggest themselves on visual
inspection of the rosettes. First, with the exception of the
innermost and outermost regions of the rosette the interstices
formed by the overlapping circles form a sort of curvilinear
rhombus (Figure 9). Not
only do all the sides of these interstices have equal length,
but all the interstices have equal length sides. Second, there
are ![]() rings
of interstices. Their aspect ratio is 1:1 in the central ring,
while moving out from this ring on either side the aspect ratio
symmetrically increases. That is, corresponding interstices on
either side of the middle ring have identical aspect ratios,
but are rotated by 90° .In contrast, the interstices of rosettes
constructed from logarithmic spirals maintain the same shape
(and aspect ratio), but only increase in size as they radiate
out from the rosette centre [Williams 1999]. As more circles
are included to make up the rosette, more interstices are naturally
created. Not only that, but the rate of change of their aspect
ratios also changes. The interstices from rosettes with very
few circles have aspect ratios fairly evenly distributed in the
range [0,1.5], whereas for rosettes containing many circles the
majority of the interstices are close to 1:1. This is verified
in the graphs in Figure 4, which show the ratios of the aspect
ratios of each ring with its inwards neighbouring ring. Due to
their perspective-like shrinking, the outer half of the rosette's
rings give the visual impression that there is a three-dimensional
spherical surface curving away from the viewer. To avoid this
and ensure that the rosette gives the impression of a starburst-like
radiating effect, many instances of circular rosette's designed
for pavements use only the inner rings, chopping off any beyond
the middle one.
rings
of interstices. Their aspect ratio is 1:1 in the central ring,
while moving out from this ring on either side the aspect ratio
symmetrically increases. That is, corresponding interstices on
either side of the middle ring have identical aspect ratios,
but are rotated by 90° .In contrast, the interstices of rosettes
constructed from logarithmic spirals maintain the same shape
(and aspect ratio), but only increase in size as they radiate
out from the rosette centre [Williams 1999]. As more circles
are included to make up the rosette, more interstices are naturally
created. Not only that, but the rate of change of their aspect
ratios also changes. The interstices from rosettes with very
few circles have aspect ratios fairly evenly distributed in the
range [0,1.5], whereas for rosettes containing many circles the
majority of the interstices are close to 1:1. This is verified
in the graphs in Figure 4, which show the ratios of the aspect
ratios of each ring with its inwards neighbouring ring. Due to
their perspective-like shrinking, the outer half of the rosette's
rings give the visual impression that there is a three-dimensional
spherical surface curving away from the viewer. To avoid this
and ensure that the rosette gives the impression of a starburst-like
radiating effect, many instances of circular rosette's designed
for pavements use only the inner rings, chopping off any beyond
the middle one.
FIVE DISKS PROBLEM
Since we have determined the intersection
points of the circles it is now easy to tackle the geometric
Five Disks Problem [Weisstein 1998] which is set as follows (see
Figure
5). Given five equally sized disks placed symmetrically
about a given centre what is the smallest radius of disk that
ensures that the radius of the circular area covered by the disks
equals one? All that needs to be done is solve ![]() with
respect to r for the given number of circles N=5,
resulting in the solution
with
respect to r for the given number of circles N=5,
resulting in the solution ![]() .We
can also determine the solution for other values of N,
and for instance find that with four circles
.We
can also determine the solution for other values of N,
and for instance find that with four circles ![]() and
for six circles
and
for six circles ![]() .
.
HYPOTROCHOIDS
It is interesting to compare the rosette
to the analytic curve called the hypotrochoid, which is generated
by tracing out a fixed point on a circle that is rolling inside
another fixed circle. The simplified form given by the parametric
equations
produces patterns very similar to circular rosettes as shown in Figure 6. The parameter q determines the number of lobes plus the equations can be modified to increase and decrease the fullness of the lobes.
One can speculate that Albrecht Dürer may also have noticed the similarity. In addition to his artistic work, he realised that mathematics could provide a powerful tool for the artist, and was interested in the connections between art and mathematics. This lead to his becoming an important Renaissance mathematician (at least in terms of early dissemination of geometry rather than an extension of the field). In his book Unterweisung der Messung mit dem Zirkel und Richtscheit he describes not only a method for designing a circular rosette floor pattern but also the construction of a large number of curves including an epicycloid (the cardioid) [Dürer 1977].
The hypotrochoid is not the only curve with similar appearance to the rosette. In fact, in 1728 Guido Grande published Flores Geometrici, which described a host of curves producing flower-like patterns.
VARIATIONS ON THE FORM
Starting from the basic circular rosette
there are many variations we can make in its construction. For
instance, the rotating circles can be replaced by other forms
such as the ellipses shown in Figure 7a. If the elongation
of the ellipses is sufficient then the interstices exhibit behaviour
somewhere in between the circular and spiral rosettes. For instance,
in the example shown the rhombus-like interstices become more
compact as they move out from the rosette centre. In comparison
with the circular rosette the variation in aspect ratio is slower.
Moreover, the aspect ratio does not reach 1:1, and so does not
contain the symmetric rings of interstices with identical aspect
ratios on either side of a middle ring. The rate of change in
interstice aspect ratio is dependent on the number of ellipses
that make up the rosette as well as their eccentricity. Therefore,
if a series of rosettes is generated in which the ellipses' eccentricity
is gradually reduced to become more circular then the ring of
1:1 interstices appears at the periphery
of the rosette and moves inwards
towards the rosette's middle ring.
Figures 7b and 7c show the effect of stretching the ellipse the other way so that it extends across the rosette rather than projecting outwards from the centre. When sufficient ellipses are included a fretwork pattern is generated in which a variety of shapes of interstices appear. Also, a circular ring is formed at the centre with radius equal to the ellipses' minor axis length. In Figures 7d and 7e, the generating circles have been replaced by superellipses [Gardner 1965] (actually supercircles since their aspect ratio is one). Due to the mixture of gently curving sides and sharper corners a more dynamic nature is created as the interstices seem to whorl into the centre from which several lotus shapes appear to emerge.
If the circular rosette is uniformly stretched in any direction this results in a rosette with an overall elliptical form (Figure 8a)[1] The rotating circles become ellipses - although varying in eccentricity unlike the identical set of ellipses making up the previous example.
Another variation on the theme of ellipses is given in the pavement in the Campidoglio which was designed by Michaelangelo (although not executed until 1940). The final version shows a more subtle construction than the above uniform stretching. The inner ring is a circle and successive rings are increasingly stretched so as to provide a gradual transition to the outer ellipse.
Other patterns can be constructed in a similar way to the circular rosette, but modifying the positions of the circles and/or their size. For instance, the nephroid and cardioid in Figures 8b and 8c retain the same positions for the circles as the rosette but their radii are a function of position.
VARIATIONS IN ARTICULATION
Again starting from
the basic circular rosette the outline can be further articulated
by various graphical means [Williams 1997]. The pavement of the
Biblioteca Laurenziana, also designed by Michaelangelo, refines
the basic rosette in two ways. It is created from the combination
of two rosettes, the second slightly rotated with respect to
the first [Nicholson and Kappraff, 1998; Kappraff 1999].
In addition, ellipses have been drawn inside the interstices.
Even simplifying the pattern to a single rosette with infinitely thin boundaries, and butting the ellipses right up to the circles still results in a difficult geometric pattern to analyse. The principal problem involves the ellipses since determining inscribed ellipses is not straightforward.
To simplify analysis we approximate the curvilinear rhombus
by a standard straight-sided rhombus (Figure
9). We can then follow the laborious procedure known
to draughtsmen for determining the inscribed ellipse to a parallelogram
[Browning 1996].[2]
In fact, for a rhombus the problem simplifies greatly. The rhombus's
and ellipse's centres are coincident, and we find that if the
lengths of the rhombus's axes are a and b, then
the lengths of the ellipse's axes are ![]() and
and ![]() and are aligned with the conjugate diameters of the rhombus.
Moreover, the ellipse's points of contact with the rhombus are
at the four midpoints of the rhombus' sides. We note that this
is also a degenerate case of the problem, solved by Newton, of
inscribing ellipses in a convex quadrilateral [Dörri 1965].
Newton found that the centres of all possible inscribed ellipses
lie on the straight line segment joining the midpoints of the
diagonals of the quadrilateral. For a rhombus the diagonals'
midpoints are coincident, and so there is a single solution for
the position of the ellipse. Nevertheless, there remain multiple
solutions for the aspect ratio. The construction we have described
maximises the ellipse's area.
and are aligned with the conjugate diameters of the rhombus.
Moreover, the ellipse's points of contact with the rhombus are
at the four midpoints of the rhombus' sides. We note that this
is also a degenerate case of the problem, solved by Newton, of
inscribing ellipses in a convex quadrilateral [Dörri 1965].
Newton found that the centres of all possible inscribed ellipses
lie on the straight line segment joining the midpoints of the
diagonals of the quadrilateral. For a rhombus the diagonals'
midpoints are coincident, and so there is a single solution for
the position of the ellipse. Nevertheless, there remain multiple
solutions for the aspect ratio. The construction we have described
maximises the ellipse's area.
As Figure 10a shows, the error caused by the approximation incurred by the straight-sided rhombus can be significant. The ellipse appears about the right size, but is shifted in towards the centre of the rosette. As the number of circles increases then the arcs making up the rhombuses' sides shorten, decreasing the total curvature. This means that the approximation error also decreases, and as can be seen in Figure 10b the ellipses fit the interstices much better.
A couple of simple corrections were tested to see if there was an easy procedure for inscribing the ellipses more accurately. The first correction is based on two corners of the rhombus that are equidistant from the rosette centre. Our original method effectively takes their average as the centre which is therefore placed closer to the rosette centre than the corners. Since it was seen that this was actually too far in, we considered pushing the ellipses out so that their centres become equidistant with the rhombus's corners. This was done by taking one of the corner points and rotating it to become aligned with the ray through the centre of the rhombus. Figure 10c demonstrates that the errors have been considerably reduced, although the ellipses are no longer in contact with their neighbours.
A second approach to the correction is to consider the maximum
error between the true circle forming the interstice and the
straight line approximation. This is ![]() where
c is the length of the sides of the rhombuses. The maximum
error occurs at the midpoints of the rhombuses' sides - exactly
where the ellipses are supposed to make contact. Pushing out
the rhombus midpoint along the ray from the rosette's centre
by this correction factor produces yet better positioned ellipses.
Even with few circles in the rosette the errors are barely visible
(Figure 10e). An advantage
of this scheme over more sophisticated ones is that since the
lengths of the interstices are all equal only a single correction
value need be calculated for the complete rosette. This also
results in the ellipses maintaining contact with their neighbours.
where
c is the length of the sides of the rhombuses. The maximum
error occurs at the midpoints of the rhombuses' sides - exactly
where the ellipses are supposed to make contact. Pushing out
the rhombus midpoint along the ray from the rosette's centre
by this correction factor produces yet better positioned ellipses.
Even with few circles in the rosette the errors are barely visible
(Figure 10e). An advantage
of this scheme over more sophisticated ones is that since the
lengths of the interstices are all equal only a single correction
value need be calculated for the complete rosette. This also
results in the ellipses maintaining contact with their neighbours.
LUNES
Each
pair of adjacent circles can be seen to produce a crescent-shaped
slice which is called a lune. One interesting aspect of the lune
is its involvement with the classic problem of "squaring
the circle". In the fifth century BC the Greek mathematician
Hippocrates succeeded in squaring the lune, i.e. he constructed
a square equal in area to the lune. Of course, while this was
an impressive feat, it did not unfortunately lead him any closer
to squaring the circle!
The inscribed ellipses can be considered as being packed into
the lunes, and their centres will lie along the middle of the
lune—its so-called medial axis. As a simpler problem we
consider lunes with inscribed circles as shown in Figure 11. This configuration
is reminiscent of the Gothic tracery in rose windows such as
that of the cathedral of Sens [Heilbron 1998]. We determine the
medial axis by finding the locus of the centres of the circles
that are tangent to both arcs of the lune. In our analysis of
the lune its bounding circular arcs are centred at (0,0) and
(0,m) and we can show that the medial axis is an ellipse
with centre ![]() and
semi-axis lengths a=r,
and
semi-axis lengths a=r, ![]() .
Setting r=1 and plotting out the medial axis's aspect
ratio a/b
for increasing values of m (in units of r),
we see that it is generally circle-like except when the lune's
two circles are so widely separated that they barely intersect
(Figure 12).
As total separation of the circles approaches (i.e. the value
of m nears 2r), the aspect ratio of the medial
axis tends to infinity.
.
Setting r=1 and plotting out the medial axis's aspect
ratio a/b
for increasing values of m (in units of r),
we see that it is generally circle-like except when the lune's
two circles are so widely separated that they barely intersect
(Figure 12).
As total separation of the circles approaches (i.e. the value
of m nears 2r), the aspect ratio of the medial
axis tends to infinity.
Of course, this degree of separation does not occur for a rosette since the most extreme case occurs when there are only three circles (although there is then no rhombus-like interstice to inscribe the ellipse within). The separation between adjacent circle centres is then 3r, which from the graph can be seen to occur just before increased separation of the circles causes large eccentricities. In fact, for the three circle case the aspect ratio of the lunes is exactly 2.
INSCRIBED CIRCLES
On investigation we find that inscribed
circles appear quite regularly, not just as mathematical problems
but in a variety of contexts spanning art and science. As previously
mentioned, they often occur in Gothic tracery. An extensive example
is given by Robert Billings who published in the nineteenth century
100 designs of geometric tracery alongside diagrams of their
construction based on four circles touching an outer circle [Billings
1849]. A few years later he continued this theme and published
a further 100 designs (see Figure
13), this time based entirely
on three inner circles, tangent to each other as well as the
outer circle [Billings 1851].
Perhaps the most famous instance of inscribed circles is that of Pappus of Alexandria, who over two thousand years ago described how to inscribe circles into the arbelos—a figure shaped like a shoemaker's knife. More recently, Dürer also took up inscribed circles as a means of dividing up a lens in an "orderly manner", as shown in Figure 14. This diagram can be generated in the following manner. Let the two circles forming the lens be centred at with radius R. The inscribed circles lie at with radius ri:
where
The equations of the circles inscribed in a lune can also be determined, although the process is more laborious (see the Appendix). This enables us to insert circles in the lunes formed by the intersecting circles making up circular rosettes, as shown in figure 15. The rosettes contain two sets of lunes; Figure 15a shows the effect of filling just one set. The circles can be seen as lying on the lunes' radiating arms. Alternatively, moving out along lune from the centre of the rosette the inscribed circles from all the lunes form a circular chain within the rosette. Although the initial circles are small, the radius of the chain is also small. Both increase until the halfway point of the lunes is reached. Thereafter the circles diminish in size while the radius of the chain continues to increase, creating more and more sparse chains. If both sets of lunes are inscribed with circles (Figure 15b) the circles intersect (except at the outermost rings), generating an additional series of lunes.
More practical applications of inscribed circles frequently occur in industrial design, often as a means of providing strength while minimising weight or material. A pair of contrasting examples can be seen in eighteenth century bridge design. In the iron bridge at Sunderland shown in Figure 16a the circles can be thought of as primarily additions to strengthen the structure.[3] On the other hand, the inscribed circles in the masonry bridge at Pontypridd (see Figure 16b) are cylinders punched through the spandrels in order to reduce weight, thus appearing as the removal rather than addition of inscribed circles.[4]
CONFORMAL MAPPINGS
Following on from the inscribed circles
described above it is interesting to note that it is possible
to transform a set of inscribed circles into a pattern reminiscent
of the rosette with inscribed ellipses that we analysed previously.
We shall apply a conformal mapping, i.e. a transformation that
preserve local angles. There are many such mappings [Kober 1957],
but we shall just consider the anti-Mercator mapping described
by Dixon [1991]. It is defined as
and its effect is to transform (diagonal) straight lines to equiangular spirals. This enables us to map translational symmetries into rotational symmetries.
Figure 17a shows seven columns of circles which are mapped
to the seven concentric rings of ovals in figure 17b. For display
purposes the top half of the columns have been clipped. It should
be noted that the ovals are egg-shaped rather than elliptical
since they contract as they approach the centre of the figure.
The circles in each column lie in the range [0, 2p];
increasing the number of circles increases the radial resolution.
Columns of circles can be added on both sides of Figure 17a extending towards
infinity, increasing the number of concentric rings in Figure 17b. Scaling the x values,
i.e. for a scaling factor s perform ![]() ,varies
the rate of radial scaling, enabling the ovals to be stretched
or squashed by any amount.
,varies
the rate of radial scaling, enabling the ovals to be stretched
or squashed by any amount.
Figure 17a also includes interstices that have been added to enclose the circles, and their mapping is included in Figure 17b. To avoid the lines crossing the circles they need to form a lattice of hexagonal elements. The mapped hexagons enclose the ovals, and expand outwards from the centre of the rosette; their two radial lines remain straight while the remaining four lines become (mildly) curvilinear. To form a pattern reminiscent of the rosette with inscribed ellipses we superimpose a grid of rhombuses through the points of contact between adjacent circles (Figure 17c). After the mapping curvilinear rhombuses are formed except that unlike the true circular rosette they cut slivers off the ovals (Figure 17d). Another noticeable difference is that this rosette behaves like a logarithmic rather than circular spiral rosette with the ovals increasing in size while maintaining the same aspect ratio [Williams 1999].
APPENDIX: INSCRIBED CIRCLES TO A LUNE
For a lune made up
from circular arcs of radius r0 we can determine the
parameters of the inscribed circles centred at (xn,yn)
with radius rn. The first circle is straightforward:
xn=0, y1=m/2, r1=m/2.
Thereafter, each inscribed circle in the sequence is found using
three constraints involving tangency with three circles: the
two that comprise the lune and the previous adjacent inscribed
circle. These can be seen as three Pythagorean triangles which
leads to three simultaneous equations, which can be solved to
give for the second circle
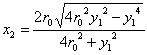
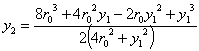
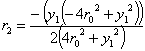
thereafter we can determine the remainder of the sequence of circles as
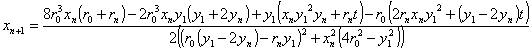
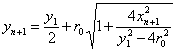
where
ACKNOWLEDGEMENTS
I
would like to thank Roger Cragg for kindly providing a copy of
his photograph of Pontypridd bridge.
NOTES
[1]
A similar figure is drawn in Phillips [1839], although it is
not further elaborated. return to
text
[2] The conjugate diameters AB and CD are drawn where AB>CD. A circle centred on the parallelogram's centre with diameter AB is drawn. A diameter EF of the circle is drawn such that it is perpendicular to AB. The angle ECF is bisected to give the orientation of the ellipse. Its final parameters, the major and minor axes lengths, are calculated as CE±CF. return to text
[3] The very first iron bridge ever built (by Abraham Darby III at Coalbrookdale in 1779) is of fairly similar design but only contains a single inscribed circle. return to text
[4] The story goes that William Edwards the builder made three attempts to build the bridge. The first bridge was swept away by a flood shortly after completion. Nearing completion the pressure of the heavy work at the spandrels caused the second to spring up in the middle. This lead to the final and successful result which was the longest single span bridge in the UK for half a century. Not only is this considered by many people to be the most beautiful arch bridge in the UK, but it is of significant engineering interest, and has gathered considerable historical and scientific analysis [Hughes et al. 1998]. return to text
REFERENCES
Billings, R.W. 1849. The Infinity of Geometric
Design Exemplified. Blackwood and Sons.
Billings, R.W. 1851. The Power of Form applied to Geometric Tracery. Blackwood and Sons.
Browning, H.C. 1996. The Principles of Architectural Drawing. Watson-Guptill Publications.
Dixon, R. 1991. Mathographics. New York: Dover. To order this book from Amazon.com, click here.
Dörri, H. 1965. 100 Great Problems of Elementary Mathematics. New York: Dover. To order this book from Amazon.com, click here.
Dürer, Albrect. 1977. The Painter's Manual - A Manual of Measurement of Lines, Areas and Solids by Means of Compass and Ruler. W. L. Strauss, ed. and trans. New York: Abaris Books.
Emerson, Ralph Waldo. 1920. Circles. In Essays, 1st series. Dent.
Gardner, M. 1965. The superellipse: a curve that lies between the ellipse and the rectangle. Scientific American 21: 222-234.
Goodyear, W.H. 1891. The Grammar of the Lotus. Sampson Low and Co.
Heilbron, J.L. 1998. Geometry Civilized: History, Culture, and Technique. Oxford: Oxford University Press.
Hughes, T.G., G.N. Pande and C. Sicilia. 1998. William Edwards Bridge, Pontypridd. Proceeding of the South Wales Institute of Engineers 106: 8-18.
Kappraff, Jay. 1999. The Hidden Pavements of Michelangelo's Lurentian Library. The Mathematical Intelligencer 21, 3 (Summer 1999): 24-29.
Kober, H. 1957. Dictionary of Conformal Representations. New York: Dover.
Melnick, M. 1994. Manhole Covers. Cambridge, MA: MIT Press. To order this book from Amazon.com, click here.
Nicholson, Ben and Jay Kappraff. 1998. The hidden pavement designs of the Laurentian library. Pp. 87-98 in Nexus II: Architecture and Mathematics, Kim Williams, ed. Fucecchio (Florence): Edizioni dell'Erba. To order this book through the NNJ, click here. To order through Amazon.com, click here.
Phillips, G. 1839. Rudiments of Curvilinear Design. London.
Rawles, B. 1997. Sacred Geometry Design Sourcebook: Universal Dimensional Patterns. Elysian Publishers.
Schmelzeisen, K. 1992. Römische Mosaiken der Africa Proconsularis - Studien zu Ornamenten, Datierungen und Werkstätten. P. Lang.
Weisstein, Eric W. 1998. CRC Concise Encyclopedia of Mathematics. CRC Press. To order this book from Amazon.com, click here.
Williams, Kim. 1997. Italian Pavements: Patterns in Space. Anchorage Press. To order this book through Amazon.com, click here.
Williams, Kim. 1999. Spirals and rosettes in architectural ornament. Nexus Network Journal 1:129-138. To order this book through the NNJ, click here.
Circles and Spheres-Geometry Junkyard
The Five Squarable Lunes
Curve Family Index
Nephroid
Hypotrochoid
ABOUT
THE AUTHOR
Paul
L. Rosin is
senior lecturer at the Department of Computer Science, Cardiff
University. Previous posts include lecturer at the Department
of Information Systems and Computing, Brunel University London,
UK, research scientist at the Institute for Remote Sensing Applications,
Joint Research Centre, Ispra, Italy, and lecturer at Curtin University
of Technology, Perth, Australia. His research interests include
the representation, segmentation, and grouping of curves, knowledge-based
vision systems, early image representations, machine vision approaches
to remote sensing, and the analysis of shape in art and architecture.
He is the secretary for the British Machine Vision Association.
|
Paul L. Rosin, "Rosettes and Other Arrangements of Circles", Nexus Network Journal, vol. 3, no. 4 (Autumn 2001), http://www.nexusjournal.com/Rosin.html |


Copyright ©2001 Kim Williams