Nikos A. Salingaros
Division of Mathematics, The University of Texas at San Antonio
San Antonio, Texas 78249 USA

Débora M. Tejada
Departamento de Matemáticas, Universidad Nacional de Colombia Apartado Aereo 3840, Medellín, COLOMBIA

INTRODUCTION
This paper tries to analyze one aspect of what is commonly understood as "modularity" in the architectural literature. We are referring to any building style that uses large, internally empty blocks or components such as rectangular panels of the same size. Where this idea is applied to define a structure's layout on the ground, or for an urban region, each unit conforms to previously fixed dimensions in a rectangular grid. At the heart of this approach lie two practices: (I) building materials are pre-fabricated only in a very limited number of sizes; and (II) one adopts a philosophy that subjugates design to empty rectangular modules. We compare here the number of choices available in different design systems. A simple model allows us to estimate the relative number of design choices in a free, non-modular design system compared to a rigid design system of empty modules.

We also compare the accuracy of approximating a given design such as a curve. This serves as an easily-grasped metaphor for design in general, where the ability to represent a complex curve depends critically on having many different scales of structure. Architects as a rule wish to have available a large number of possible solutions, so as to enhance their ability to generate novel designs. Working within a modular system of design (with or without supplementary conditions such as internal structure in a module), however, restricts the number of possible results in a drastic manner. The restriction imposed by empty modularity may eliminate all of the possible designs that relate visually and functionally to human beings. We will argue that using empty modules reverses ancient practices that lie at the basis of humanity's connection with nature.

The alternative to modular design is creating a form through subdivision or differentiation. A structure and its components can in this way have any dimension or shape, and at the same time, the structure can utilize materials in a variety of sizes and shapes. Design can be freed up by subdividing the building materials to achieve a spatial coherence as determined by human functions, movement, the psychological perception of space, connectivity, etc. This is the opposite from rigidly fitting human functions into a geometrical frame that is determined primarily by the size of pre-fabricated construction panels. Today we try to fit ourselves into some arbitrary dimensions fixed by an architect without any regard for the complexity of our spatial and emotional needs.

Modular arrangements often define the aesthetics of a "style". Reasons for adopting a modular design system in architecture include those of economy of thought and action: it is easy to repeat a design unit that has worked before. It is true in almost all architectures, including various vernacular traditions, that a style is defined after a successful modular system has been developed, which is then formalized into a design canon such as the Classical orders. For example, the transition from wooden to marble construction in early Greek architecture occurred after the former material was developed into a successful system for building temples. The resulting style re-makes sensible wooden modules out of marble, which is not all that practical, even though the results are wonderful.

GOOD AND BAD APPLICATIONS OF MODULARITY
Classical, Romanesque, and Gothic Architectures are characterized by the repetition of large geometric modules such as bays, columns, windows, etc. These elements possess internal substructure (decoration, fluting, borders) even though some of the smaller modules -- such as the ordinary brick and smoothed stones -- are visually empty. Certain modular elements that are used in Classical and traditional buildings could be described as undecorated, yet there exists decoration on that and smaller scales elsewhere in the building. The result is a visual balance between substructure on many different scales, which follows from a fundamental mathematical rule on the relative number of subelements in a structure [Salingaros and West 1999].

Qualitatively, the result of the study by Salingaros and West [1999] may be stated as follows: "Substructure exists in a hierarchy that follows an inverse proportionality: many smaller subelements; fewer intermediate ones; and very few larger ones". This multiplicity rule, derived for general complex structures, explains why contemporary neoclassical buildings don't always achieve the appropriate visual impact. Their forms clearly refer to classical forms, but the distribution of subdivisions is closer to the early modernists such as Mies van der Rohe and Le Corbusier. That is because substructure is cut off at a relatively large size; or if smaller elements are present at all, they are not numerous enough for visual balance. For this reason, despite an obvious attempt to mimic Classical prototypes, recent neoclassical buildings tend to resemble in spirit the modernist buildings they are trying to contrast with.

Looking at the architectural and urban failures of the twentieth century, modularity is one candidate for critical scrutiny since ugly, boring buildings look the same, and many of them consist of large empty rectangular panels or exposed untreated concrete, and lack ornament and color. The distribution of sizes is cut off at the size of the empty modules and so the scaling does not continue downwards. Thus, the mathematical connection of the structural scales to the scales of human perception and movement, all the way down to the minute scales present in natural materials, is eliminated. The worst urban mistakes are again characterized by rectangular blocks arranged in precise modular alignment. The more such buildings repeat, the more they create an inhuman habitat whose negative effect is proportional to the area covered by the modules.

The deficiencies of uniformity become dramatic on the urban scale. The requirements of totally different functions would normally preclude mixed-use building groups from sharing the same module, yet the industrial production of the same modules encourages architects to create similar buildings and monotonous urban zones. The alternative is to abandon a pointless strict modularity on such a large scale. Instead of doing that, however, we have eliminated mixed use and variety, partly in order to preserve a visual geometrical modularity on the urban plan. Modularity applied in this manner thus concentrates functions. Our cities now assume their form based on visual templates that are totally alien to the complexity of human perception, functions, and movement.

A free design process that allows for numerous subdivisions permits mathematical substructure on many different scales. By abandoning an empty modularity, one has access to solutions based on a far richer approach to design that creates visually successful buildings. Art Nouveau architects like Antoni Gaudí used small modular elements (such as standard bricks) to create curved large-scale structures. This freedom of form contrasts with those instances where a building reproduces the shape of an empty rectangular module. The small scale can link to the large scale mathematically, because scaling similarity in design is a connective mechanism of our perception. Therefore, the materials can and do influence the conception of the large-scale form, and the larger a module, the stronger the influence. When one chooses to use large, empty rectangular panels, these will necessarily influence the overall building; often implying a monotonous, empty rectangular façade.

CHRISTOPHER ALEXANDER'S OFFICE DESIGN SYSTEM
Christopher Alexander has written one of the most perceptive articles on modularity and proportional ratios in architecture [Alexander 1959]. Much later, he introduced a novel, human-oriented design system for office furniture and layout [Alexander, et al. 1987]. These ideas were developed further in a project for the furniture maker Herman Miller (as described in Alexander 2000). After thinking about the general problem of accommodating personal needs in an office environment in terms of the built components, Alexander concluded that the modular system of standard-size furniture and office units is far too restrictive. He realized that such a system can never hope to satisfy the personal needs of an individual in an office (or any other) environment. The solution was a more flexible system that broke out of modularity, and which enabled each person to choose their own dimensions for furniture, and especially for spaces.

In describing the user-layout design process, Alexander says:

It is essential to stress that this process is entirely different from the layout process available in computerized systems using modular components. These systems allow the user to arrange and rearrange the modules. Our research shows that any process of arranging and rearranging modules is fundamentally limited, and cannot produce the kind of comfort -- the deep and simple feelings -- that we are seeking. ... Profound adaptation in which things are comfortably related to one another can only occur when the elements involved are all capable of very fine dimensional variation. ... The aspect of the layout process itself which is necessary to make this non-modularity work is that it is a process of differentiation (similar to the process of embryonic development) in which the parts are gradually differentiated from the whole -- instead of the whole being made up from modular parts [Alexander, et al. 1987]

Realizing that this result is fundamental for all design (and is not just restricted to office layout and furniture), Alexander has developed it at length in his new book, The Nature of Order, which details a comprehensive theory of order. We include a few of Alexander's comments from that book, describing his office design system in more detail:

The arrangements that people created in this way were genuinely personal, genuinely well-adapted to the rooms ... They were altogether different in character from the stiff, and usually unworkable arrangements that could be created by arranging the standard components in a few rigid arrays. ... My program worked by differentiating space, and allowing different objects to crystallize out from the space, in the shape and size they needed, for their particular role ... Why was I convinced that the infinity of configurations created by differentiation in my system, was a richer and larger infinity than the infinity of geometrical arrangements that could be made by arranging and re-arranging standard components? [Alexander 2000].

The derivation presented in the following sections answers Alexander's question, and proves his intuition correct.

THE NUMBER OF DESIGN CHOICES IN A MODULAR DESIGN SYSTEM AS COMPARED TO A NON-MODULAR DESIGN
We now show that the number of design possibilities obtainable from a free, non-modular system is infinitely times more than the number of all design possibilities obtainable from a comparable modular system. This remains true even as the size of the module becomes infinitesimally small.

While the eye and mind cannot actually perceive the difference between a very large number and an infinite number of different objects, a person can indeed experience a responsive design when compared to other designs that are deficient in some way. It may be difficult to put one's finger on what is lacking in a particular building, yet the fact that one experiences a visceral, positive emotional experience in a great historical building is incontrovertible. The point we are trying to make is that placing restrictions on design, as a modular system certainly does, might well eliminate the few optimal design solutions for that project. In particular, the vast majority of the world's favorite buildings -- representative of all periods of architecture, and coming from different stylistic traditions and geographic regions -- are excluded by a modular system of empty units.

Counting the possible arrangements of modular units in a design is a straightforward exercise. Without any loss of generality, we construct a one-dimensional model where the proof is much easier to follow. Consider a line of length equal to one on some arbitrary scale. The length of the line is going to correspond to the size of a building or urban ensemble. We are going to imagine n design units or components that can be laid in a row and entirely fill up the line. Each unit labelled i has length x(i) , and the sum of all the x(i) equals one (the length of the line). This arrangement can be thought of as a particular subdivision or partition of the line.

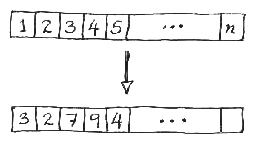
Figure 1. A one-dimensional model. Each distinct modular design corresponds to one particular arrangement of n numbers along a line.

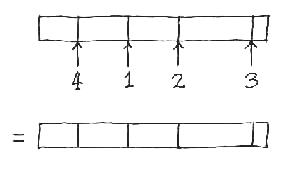
Now we ask: how many possible re-arrangements of these n elements are there? That is, in how many distinct ways can we shuffle these n elements, not necessarily all of the same length, along the line? The answer comes from combinatorics, and equals n! , where the factorial notation means n! = 1.2.3. ... .(n - 1).n . For example, if there are 5 distinct elements that make up the line, then the number of possible re-arrangements is 5! = 120. Clearly, as the number of discernible units making up the line increases, the number of possible combinations becomes large.

We will use the analogy that each re-arrangement of the units making up the line corresponds to a particular design solution. It follows that the total number of possible re-arrangements equals the number of design possibilities inherent in this design system. In practice, however, architects working with modular design usually define only one basic unit, which is the single module, so that all the units are indistinguishable and of the same size, x(i) = 1/n . If we have n copies of the same unit, then the number of possible re-arrangements equals exactly one -- since all re-arrangements lead to the same result -- so there is only one choice.

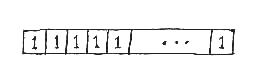
THE NUMBER OF NON-MODULAR POSSIBILITIES
When one is not constrained to work with pre-defined units, then one has complete freedom to make up elements as the design progresses. The components can be made any desired size, by subdividing or fitting within the already decided larger dimensions. To show this in a one-dimensional model, start with a line of length one and subdivide it to define n elements, as follows. With a clean line, make one mark that divides it into two segments. A second mark divides the line into three segments, and proceed in this manner until after n - 1 marks we have n segments. These n - 1 marks generate an n-element partition of the line, which is analogous to the partition defined in the preceding section. To create a different partition in the free design scheme, one merely subdivides at (some) new points.

We now count the number of possible ways to affect such a partition. There exist an infinite number of possibilities of where to place the first mark, since it can be made anywhere on the line. Once we start, the positions of the second and all subsequent marks also have an infinite number of possibilities. Altogether, therefore, each partition of the line into n segments has possibility equal to infinity to the power n - 1 , which equals infinity. This counts the number of ways in which a line can be partitioned into n segments. In a non-modular design system where shapes are defined freely, we have a genuinely infinite number of solutions.

THE LIMIT OF n BECOMES INFINITE
A practitioner is drawn to use as large a module as possible in order to obtain the presumed economical advantages of a modular design system. When justifying such a system, however, proponents of modularity turn instead to the opposite case of theoretically small modules, where the number of modules n increases. This is misleading for two reasons.

Shrinking the size of the basic units increases the number of different units, hence the number of design possibilities. The re-arrangements in our one-dimensional model become more numerous as n increases, but one never recovers the design freedom of a non-modular system. A common error is to assume that as something becomes infinite, one can cancel with another infinity to get a result of one. In fact, the ratio of modular to non-modular choices equals n!/ƒ = 0 for all n , so the limit as n goes to infinity is the limit of the sequence { 1/ƒ , 2/ƒ , 6/ƒ , ... }, which is equal to { 0, 0, 0, ... }. The terms of this sequence never change from zero. From the theory of transfinite numbers, the ideal case of a modular system with an infinite number of distinct infinitesimal units does allow an infinite number of choices, but a non-modular system allows a higher-order infinity of choices. The second, larger infinity is the exponential of the first, smaller infinity. In the case of a single modular unit, as in a minimalist design style, one still has a single choice compared to infinity.

FRACTAL GEOMETRY AND MATERIALS
Fractals are often thought of as singular, artificial constructions, exemplified by multicolored pictures of spirals such as the Mandelbrot set generated by a computer. This popular conception overlooks the fact that fractals are overwhelmingly the model used by nature for constructing forms, both living and inanimate [Mandelbrot 1983]. Fractal designs are everywhere: they include trees, animals, snowflakes, folk art, buildings, cities, and human artifacts. Far from fractals being exceptional, the vast majority of natural structures is fractal [Ball 1999]. Fractals encompass everything that is alive, as well as much of inorganic matter. It is principally man-made objects from the twentieth century that have deliberately non-fractal qualities.

A fractal's substructure is evident at every magnification, so that at no scale is the structure empty. This represents the opposite of a simplistic geometry of rectangular blocks, where structure is defined on only two scales, usually those of the module and the overall size of the building. An important feature of all fractals is that they satisfy the multiplicity rule for the distribution of subelements [Salingaros and West 1999]. Natural processes generate subelements in inverse proportion to their size. Material stresses create fractures that show as regular or irregular patterns, which prevent a continuous ordering throughout the form. Initially smooth materials will generate a fractal structure over time [Ball 1999]. Pure, non-fractal objects are unstable under weathering, which is precisely the reason they are not often found in nature.

Modularity in design is related to the use of non-weathering materials in the following way. As explained above, natural forces and weathering generate substructure, thus destroying scale dominance [Ball 1999]. If we create an artificial non-fractal structure by emphasizing one particular scale -- say, the scale of a plain module -- then we are violating natural processes. To be in any way effective, such structures must resist weathering. It is for this reason that the topics of modularity, geometrical purity, and non-weathering materials are inextricably bound together. A preoccupation with shiny, smooth, or transparent materials follows the desire to avoid fractal substructure. It is well known that early modernist architects founded their new style of building on a search for "new" materials that they hoped would not weather at all.

Going upwards in scale, same-size elements in nature tend to join in higher-order groupings. Units of similar size connect into superstructures or communities. Forces are distributed among many different scales, thus ensuring a more efficient linking. The emergence of higher scales corresponds to upward fractal growth, a process that guides morphogenesis and creates complex order while minimizing randomness. The separateness of repeated units existing on one scale is sacrificed to the coherent structure of a higher scale. This generative process is reversed by empty modularity, which tries to maintain the emptiness of its original module with no internal substructure. Architectural modules of this type are often used to build an empty scaled-up version of the module.

An inanimate object can have different degrees of organized complexity. There is a process by which this complexity is developed and maintained. We repair buildings and the urban fabric from wear and tear and physical decay, which is analogous to the feeding and maintenance of organisms or machines. The difference is that in artificial systems as opposed to biological systems, repair is done by human beings rather than by the entities themselves. A structure that doesn't weather at all appears alien to a human being. For buildings to weather well, they have to allow for the development of a fractal structure: they must be designed from the beginning with a fractal hierarchy of scales, otherwise the inevitable patterns that develop as a result of weathering will cut across the original design intentions. The only way to prevent this inconsistency is to anticipate a fractal form in the original design.

APPROXIMATING CURVES AS A METAPHOR FOR DESIGN FREEDOM
With an increase in the number of components, there is a corresponding increase in the number of intermediate levels of structure. Structural complexity arises from the process of adding components on different scales, with linking and coupling between all those components, and on all scales. The opposite is empty simplicity, which is achieved by eliminating all substructure.

We propose to link ordered complexity as characterized by levels of substructure, on the one hand, to design freedom, on the other. This can be seen in the simplest design problem: creating a curved surface to accommodate human movement, psychological space, or other factor optimizing people's physical and emotional interactions with a building. We will show that a non-trivial curve cannot be constructed without abandoning the simplistic modularity discussed earlier.

Any curve can be obtained as an approximation of straight segments of connected lines. Nevertheless, a good approximation depends on the length of the basic segments that are utilized. In a modular system of several elements, one of them with a fixed length is going to be the smallest. The size of the smallest element limits the curvature of curves that can be approximated. Consider the case of a single module. Comparing the three approximations to a semi-circle shown here, we observe for example that the possibility of creating an accurate representation of a smooth circle of given radius gets better as the length of the modular segment becomes smaller.

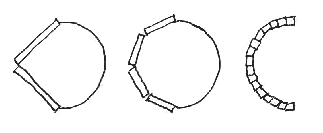
One might think that approximating curves can be improved by introducing modules with curvature. We could then have arcs of different length and curvature. In contrast to the case of the straight segments, however, the curves with greater curvature will not necessarily be better approximated by the smallest modules of arc. The approximation is still limited by the length and shape of the modular segment. Neither approximation shown below is particularly satisfying, which reveals the inadequacies of any modular design system. This can be remedied by combining small and large units of different curvature together. Different units will fit different sections of the curve. This results in by far the most accurate representation of a continuous figure by means of an encoding scheme. We are thus led away from strict modularity, and into fractal approximation that works on many different scales simultaneously.

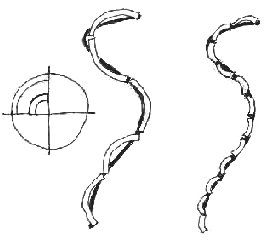
After this simple analysis, we can see why modular architecture abandons curved designs on the smaller scales: the reason is that realizing a curve using relatively large modules is mathematically impossible. Complex designs require components on different scales. Empty modularity restricts the curvature of design, and so empty modularity is incompatible with mathematically-rich designs such as curves. Thus, the architecture of rectangular modules eliminates one of the principal components of natural forms. We identify this exclusion as a major reason for the dull uniformity of rectangular boxes. Recent buildings such as the Denver airport and the Bilbao Art museum take advantage of new materials and computer-aided design and fabrication to break out of the rectangularity inherent in the old early modern mechanical reproduction of many identical components.

The metaphor of approximating a complex curve shows the need to allow for different structural units at different scales. A building need not be curved necessarily, yet it should ideally follow a similar design freedom: the geometry must arise from subdivision rather than modular juxtaposition. We thus propose a metaphor for design that in general responds better to human physical and psychological needs. The freedom necessary to achieve those aims requires the ability to adjust the built form according to complex inputs. If we follow a rigid visual image too faithfully, we cannot at the same time create a design plan that serves unanticipated but important needs. The reason for this contradiction is the impossibility of predicting in advance all the uncountable effects and interactions between human beings and the built form.

MODULARITY AND MASS PRODUCTION
Modularity in design was spurred by mass-production techniques in manufacturing, in an attempt to simplify production and reduce building costs. American mass production began first in the small arms industry, then spread to domestic machines. Henry Ford introduced the production line in 1913 to mass-produce cars. Buildings were being modularized and industrialized from the beginning of the nineteenth century, with cast iron warehouse construction, balloon frame houses, etc. Architects, beginning in the 1920's, examined the possibility of emulating Ford's methods in the building industry. Nevertheless, with the exception of a few housing systems, mobile homes, and caravans, there has never been a successful production line in architecture. Large-scale experiments in prefabricated housing after World War II mostly ended in failure.

The idea of modularity was never abandoned, however, and it has strongly influenced the design of twentieth-century buildings around the world. Even if whole buildings could not be successfully mass-produced, architects felt that the old-fashioned way of tailoring each piece of a building to fit individual uses and shapes, as was often done in the past, was no longer permissible. This ideology led to the standardization of many building measures and components: low ceiling heights for apartments; fixed sizes of doors and windows; plumbing and lighting fixtures; wall panels; etc. In commercial buildings, modularity went as far as it could go without actually mass-producing complete units such as bathrooms.

Modular construction was accepted by the post-war architectural community as a necessary component of building for the future. We have inherited the idea of modular design in a watered-down version that leads to the most boring and minimally satisfying results. Today, both apartments and tract houses tend to be built throughout a region according to standardized plans; not an optimized plan for patterns of family life and climate as in vernacular architecture, but simply a dimly-remembered floor plan from the heady days of early modernism. Housing "developments" usually repeat a single poorly-adapted house plan with only minor variations, which moreover offers few of the advantages of modular construction. Such houses are still built by hand, using the cheapest possible materials.

A rectangular grid exists in countless examples of post-war buildings and construction. We mention here the 3 ft. 4 in x 8 ft. 3 in planning grid used in England by the Hertfordshire school system, and the 3 m x 3 m grid used by Constantine Doxiades in building several new villages in the Arab world. Ludwig Mies van der Rohe employed an empty module of 24 in x 33 in for the 1950 Farnsworth house. People continue to think that there is something fundamentally advantageous to such a restriction, which is questionable. It might look more efficient on paper, but it does not lead to life in the built environment. Le Corbusier wrote at length on the presumed advantages of a Cartesian grid in his own journal, L'Esprit Nouveau, giving colorful arguments. The visual force of his crisp drawings was enough to establish the modular orthogonal grid in the minds of architects and planners.

Among the few modernist architects who refused to adopt modular design in buildings as a matter of principle was Alvar Aalto, who is reported to have said: "my module is the millimeter". Even the organic post-modernist architecture of Lucien Kroll was praised for using a 10 cm module previously developed by the Dutch group Stichting Architectural Research (SAR). Kroll says, however, that: "... even 10 cm is too large; 2.5 cm or 1 cm would be more ideal" [Kroll 1987: 59]. Empty rectangular modules should not be confused with translational symmetry in older buildings, because the design intents are the opposite. Joseph Paxton's 1851 Crystal Palace uses a structural frame of 24 ft x 24 ft. It is misleading to claim that the 13C Amiens Cathedral is modular because it has a clearly-defined frame at 23.5 ft x 23.5 ft. This is obviously not an empty module, but contains an extraordinary wealth of further structure on smaller scales.

CONCLUSION
There are arguments to be made in favor of modularity, but not for the way it is used in many buildings. If we have a large quantity of structural information, then modular design can organize this information to prevent randomness and sensory overload. In that case, the module is not an empty module, but a rich, complex module containing a considerable amount of substructure. Such a module organizes its internal information; it does not eliminate it. Empty modules, on the other hand, eliminate internal information, and their repetition eliminates information from the entire region that they cover. Modularity works in a positive sense only when there is substructure to organize. One aim of this paper was to correct certain misconceptions that date from applications of mathematics to architectural design, giving the impression that using rectangular modules is somehow more scientific. That is not true. We argued against empty modularity, using mathematics to prove our point.

ACKNOWLEDGMENTS
Professor Tejada spent her sabbatical year 1999-2000 at the University of Texas at San Antonio, supported by a grant from the Alfred P. Sloan Foundation. Both authors thank the Alfred P. Sloan Foundation for support.

REFERENCES
Alexander, Christopher. 1959. "Perception and Modular Co-ordination." Pp. 425-429 in Journal of the Royal Institute of British Architects 66.

Alexander, Christopher, A. Anninou, G. Black and J. Rheinfrank. 1987. "Towards a Personal Workplace." Pp. 131-141 in Architectural Record Interiors, Vol. Mid-September .

Alexander, Christopher. 2000. The Nature of Order (New York: Oxford University Press). (in press.)

Ball, Philip. 1999. The Self-Made Tapestry (Oxford: Oxford University Press). To order this book from Amazon.com, click here.

Kroll, Lucien. 1987. An Architecture of Complexity (Cambridge, MA: MIT Press).

Mandelbrot, Benoit B. 1983. The Fractal Geometry of Nature (New York: Freeman). To order this book from Amazon.com, click here.

Salingaros, Nikos A. and Bruce J. West. 1999. "A Universal Rule for the Distribution of Sizes." Pp. 909-923 in Environment and Planning B: Planning and Design 26.

ABOUT THE AUTHORS
Nikos Salingaros (Ph. D. Physics 1978, State University of New York at Stony Brook) is Professor of Mathematics at the University of Texas at San Antonio. He is the author of more than 70 scientific papers on mathematical physics, thermonuclear fusion, and complexity. After working for many years in mainstream scientific topics, he was influenced by Christopher Alexander to turn his attention to architectural problems. His current research interests focus on deriving a mathematical foundation for architecture and urban planning. This research program is supported in part by a grant from the Alfred P. Sloan Foundation.
Débora M. Tejada (Doctorate in Algebra 1981, University of Montpellier, France; Ph. D. in Topology 1993, University of North Texas, Denton) is Professor of Mathematics at the Universidad Nacional de Colombia, in Medellin. During the academic year 1999-2000, she was a visitor in the Mathematics Department at the University of Texas at San Antonio. Dr. Tejada's principal publications are in the area of Knot Theory. Recently she has become interested in the mathematical foundations of Architectural form and Urbanism.

Copyright ©2001 Kim Williams