| "Triangulature" in Andrea Palladio |
|---|
Center of Mathematics and Design (MAyDI)
University of Buenos Aires, Argentina
In a paper published in the Journal of the Society of Architectural Historians [1], the Serbian Branko Mitrovic claims that in Palladio's plans there exist six unexplained ratios that are close to the ratio Ö3:1, with the closest being the four large corner rooms of the Villa Rotonda (Figure 1 and Figure 2).

Figure 1. Photo of the exterior of Palladio's Villa Rotonda. Reproduced by courtesy of Stephen R. Wassell.
Figure 2. Plan and elevation of the Villa Rotonda, from Andrea Palladio, I quattro libri dell'architettura, Book II.
Each corner room has dimensions 26 x 15, which differ from the actual ratio Ö3:1 by only 0.07%! This astonishingly close approximation could be a very good reason for suggesting that Palladio used, on some occasions, a system of proportions based on the height of the equilateral triangle, or "triangulature".
But the numbers 26 and 15 in the drawings of the Rotonda were not chosen arbitrarily. In fact, let us look for the positive solution of the quadratic equation
|
|
(1) |
It can be written in the form
|
|
(2) |
or, dividing by x (different from zero)
|
|
(3) |
Then it is possible, by substitution of x = 4 - (1/x) to get the continued fraction equation
 |
(4) |
where we have relaxed the condition that the terms of the continued fraction have to be positive [2].
Let us now introduce the notation
for this purely periodic continued fraction expansion.
The positive solution of equation (1) is
|
|
(5) |
from which we get:
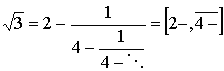 |
(6) |
This periodic continued fraction expansion has the following rational approximants:
s (2) = 26/15 = 1.7333...;
s (3) = 97/56 = 1.7321428...;
s (4) = 362/209 = 1.7320574...
Comparing these results with the exact value = l.7320508..., we note that the second rational approximant 26/15 is exact to two decimal places. The third one is exact to four decimal places and the fourth to five decimal places!
This continued fraction expansion of Ö3, in which the approximants are by excess, is much better than the usual one [3]:
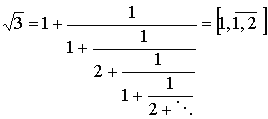 |
(7) |
that has the following rational approximants:
s (2) = 5/3 = 1.666...;
s (3) = 7/4 = 1.75;
s (4) = 19/11 = 1.7222...
It is easy to notice that in this case the fourth rational approximant is only exact to one decimal place!
In the case of Ö3, we may ascertain this curious behavior of getting a much quicker convergence with a continued fraction expansion that approximates by excess than the simple continued fraction expansion. I am not sure if this happens with every square root of a natural number, but it certainly happens with the square roots you find by looking for the positive solutions of quadratic equations of the type
where n > 0 is natural number. This is the subject of the research I am now undertaking.
REFERENCES
[1]
Branko Mitrovic, "Palladio's Theory of Proportions and the
Second Book of the Quattro Libri dell 'Architettura",
Journal of the Society of Architectural Historians 49,
3 (September 1990): pp. 279-292. back
to text
[2] Oskar Perron, Die Lehre von den Kettenbrüchen (Leipzig and Berlin: B. G. Teubner, 1929). back to text
[3] C. D. Olds, Continued Fractions (Washington, DC: Mathematical Association of America Books, 1963. back to text
FOR FURTHER READING
Vera W. de Spinadel, "The Metallic Means and
Design", Nexus II: Architecture and Mathematics,
Kim Williams, ed. (Fucecchio, Florence: Edizioni dell'Erba, 1998),
143-157.
Stephen R. Wassell, "The Mathematics of Palladio's Villas", Nexus II: Architecture and Mathematics, Kim Williams, ed. (Fucecchio, Florence: Edizioni dell'Erba, 1998), 173-186.
RELATED
SITES ON THE WWW
Palladio's
Italian Villas
The
Palladio Museum
An
Itinerary of Villas and their Commissioners
Life of Palladio
Villa
Rotonda
Villa
Poiana
Villa
Pisani
Geométrica:
Arquitetos: Andrea Palladio
ABOUT THE AUTHOR
Vera
W. de Spinadel is a Full Consultant Professor at the Faculty
of Architecture, Design and Urbanism at the University of Buenos
Aires, Argentina. She is the Director of the research centre
Mathematics and Design, which comprises a team of interdisciplinary
professionals working on the relations amoung Mathematics and
Informatics with Design, where the word "design" is
understood in a very broad sense (architectonic, graphic, industrial,
textile, image and sound design, etc.). She organized the First
and Second International Conferences on Mathematics and Design.
She is the author of several books and has published many research
papers in international journals. She has received several research
and development grants as well as several research and technological
production prizes. return to top
|
Vera de Spinadel "Triangulature" in A.Palladio , Nexus Network Journal, vol. 1 (1999), pp. 117-120. http://www.nexusjournal.com/Spinadel.html |
Copyright ©1999 Kim Williams

