
| Book Review |
|---|
Rezension des Buches: Klaus Schröer / Klaus Irle: "Ich aber quadriere den Kreis..." - Leonardo da Vincis Proportionsstudie, Waxmann Verlag, Münster / New York / München/ Berlin 1998. Jetzt kaufen von Amazon.de!
Lerchenweg 3
D-34233 Fuldatal
 Der
Titel des Buches "Ich aber quadriere den Kreis..."
zitiert Leonardo selber (Windsor 12280 r, 1508-9; S. 37) mit
einer Bemerkung über Archimedes, der „ein Vieleck quadriert,
aber nicht die Fläche eines Kreises" ("adunque
archimenjde non quadra maj figura di lato curvo"; S.18).
Leonardo betont sein Vorhaben, wirklich gekrümmte Figuren
zu quadrieren. Die Autoren beziehen sich dabei auf mehrere Belegstellen,
wo Leonardo seine Überzeugung ausdrückt, mit Zirkel
und Lineal eine rein geometrische Methode der Kreisquadratur
entwickeln zu können: Die Rekonstruktion der Verfasser zeigt
am Ende dieses geometrischen Prozesses eine gute Annäherung
von 1,000373 zwischen der Kreisfläche und der des Quadrates
mit der Seitenlänge der Einheit 1. Aber man findet in Leonardos
Schriften über Mathematik, Geometrie und Kunsttheorie keinen
Kommentar oder eine Erläuterung zu diesem Vorhaben, nur
einige andere Versuche von Kreis- und Quadrat- Schnitten mit
verschiedenen Andeutungen zur Kreisquadratur.
Der
Titel des Buches "Ich aber quadriere den Kreis..."
zitiert Leonardo selber (Windsor 12280 r, 1508-9; S. 37) mit
einer Bemerkung über Archimedes, der „ein Vieleck quadriert,
aber nicht die Fläche eines Kreises" ("adunque
archimenjde non quadra maj figura di lato curvo"; S.18).
Leonardo betont sein Vorhaben, wirklich gekrümmte Figuren
zu quadrieren. Die Autoren beziehen sich dabei auf mehrere Belegstellen,
wo Leonardo seine Überzeugung ausdrückt, mit Zirkel
und Lineal eine rein geometrische Methode der Kreisquadratur
entwickeln zu können: Die Rekonstruktion der Verfasser zeigt
am Ende dieses geometrischen Prozesses eine gute Annäherung
von 1,000373 zwischen der Kreisfläche und der des Quadrates
mit der Seitenlänge der Einheit 1. Aber man findet in Leonardos
Schriften über Mathematik, Geometrie und Kunsttheorie keinen
Kommentar oder eine Erläuterung zu diesem Vorhaben, nur
einige andere Versuche von Kreis- und Quadrat- Schnitten mit
verschiedenen Andeutungen zur Kreisquadratur.
Das Buch ist eine Zusammenarbeit eines Kunsthistorikers (Dr.
Klaus Irle) und eines Künstlers, der bewußt mit mathematischen
Formen und Lösungen arbeitet (Klaus Schröer). Sie weisen
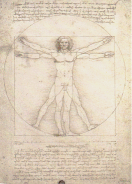
nach, daß die bekannte und berühmte Zeichnung des
"Vitruv-Mannes" von Leonardo über 500 Jahre als
die Renaissance-Studie menschlicher Proportionen nach den Regeln
und Maßangaben Vitruvs verstanden wurde. Dabei wurde die
mathematische Tatsache nicht wahrgenommen, daß in der Zeichnung
auch (oder eigentlich?) ein rein geometrisches Konzept
der Kreisquadratur enthalten ist, die Leonardo in der Analyse
menschlicher Proportionen entdeckte. Aber diese "verborgene
Aussage" der Zeichnung ist (möglicherweise bewußt)
verschlüsselt worden und niemand bemerkte dies in den letzten
5 Jahrhunderten Rezeptionsgeschichte aus hauptsächlich wohl
zwei Gründen:
1) Die Kunstgeschichte der
letzten beiden Jahrhunderte nahm die enge Beziehung zwischen
Mathematik und Kunst der Renaissance, die auf der Kenntnis der
antiken Schriften beruhte, nicht zur Kenntnis (Panowsky, 1940;
Ost, 1975; Kemp, 1981; Zöllner, 1987; Braunfels Esche, 1994;
p.67 ff.).
2) Die Kunst desselben Zeitraumes definierte
sich in der Betonung von Gefühlen und subjektiven Wahrnehmungen
des Künstlers und war nicht bestimmt von ewig gültigen
mathematischen Regeln, Rahmenbedingungen und Gesetzen, um ein
Abbild der "objektiven" Wirklichkeit zu schaffen.
Folgerichtig bemühen sich die Autoren um eine
Wiederbelebung dieser Aspekte in der Kunsttheorie der Renaissance
besonders für die Malerei und ihre Beziehungen zur Mathematik.
Leonardo, der als "Universal-Genie" ein umfassendes
Forschungsspektrum auf den Gebieten der "Mathematik, Anatomie,
Mechanik, Hydraulik, Geologie, Astronomie, Zoologie, Botanik
und Maltechnik" aufzuweisen hat, füllt mit seinen Bänden
und deren Kommentierung die Bibliotheken von Mailand, Turin,
Rom, Paris, London, Oxford, Madrid, New York und Los Angeles.
Seine Hydraulik-Studien sind vollständig im Privatbesitz
von Bill Gates (Microsoft). In den gesammelten Codices findet
man zwar viele Bemerkungen Leonardos zu mathematischen Versuchen
(einschließlich der Kreisquadratur), aber die Zeichnung
des "Vitruv-Mannes" wurde bisher nie im mathematischen
Kontext der 3 berühmten antiken "mathematischen Rätsel"
interpretiert und analysiert (Dreiteilung des Winkels, Verdoppelung
des Würfels, Quadratur des Kreises).
Um das dazu gehörige "Regelwerk" zu verstehen,
ist es zunächst nötig, die Textversion Vitruvs mit
dem Kommentar Leonardos zu seiner Zeichnung und ihre eigene Aussage
zu vergleichen; denn es gibt 3 wichtige Unterschiede:
1.
Leonardo spreizt die Beine des Mannes genau bis zu 1/14 seiner
Größe. Vitruv weist hierzu keine Berechnung auf.
2. Nach Leonardo sind die Arme genau bis zur den
Kopf begrenzenden Linie erhoben, so daß seine Fingerspitzen
diese (Kopf-) Linie berühren. Dazu bemerkt Vitruv nichts.
3. Mit dieser Position der Glieder bedeutet die Spanne der gespreizten
Beine ein gleichschenkliges Dreieck. Man findet bei Vitruv nichts
darüber.
Außerdem gibt es Unterschiede
in der Aufteilung einzelner Körperdistanzen zwischen V.
und L.: Leonardo setzt die obere Brust-Linie als den 6. Teil
der Körpergröße an, Vitruv berechnet 1/6 + 1/40.
Vitruv bemißt die Körpergröße mit 6 Fuß,
Leonardo aber mit 7 Fuß. Das bedeutet, daß Leonardo
eine neue Proportionsstudie unter Bezug auf die antike Version
des Vitruv geschaffen hat. Und genau mit dieser Veränderung
ist es möglich, einen geometrischen Prozeß der Kreisquadratur
(mit hoher Annäherung) zu bewerkstelligen.
Nach meiner Meinung demonstriert Leonardo diese Überbietung Vitruvs, indem er dessen Text oberhalb der Zeichnung in gewisser Weise optisch "hinter" seine eigene Zeichnung zurücktreten läßt. Die Zeichnung grenzt ihn so aus, daß es scheint, der Kreis verdecke den alten Text; demgegenüber ist Leonardos eigener Text mit gleichsam einer Überschrift versehen und durch die Maßkette deutlich vom Bild getrennt (Abb. S. 104). Die Verfasser sehen in dieser Kombination von Text und Bild einen Zusammenhang zur sogenannten "emblematischen Kunst" des 15.-17. Jh., eine kleinformatige Literaturgattung mit einer "Überschrift" (Vitruvs Text), einem "Bild" (Leonardos Zeichnung) und einem "erläuternden Text" (Bildkommentar Leonardos darunter). Aber dieses Genre diente ursprünglich einer Popularisierung moralischer Werte, ethischer Normen und lebensphilosophischer Ratschläge in einer elementarisierten Form, so daß auch ungebildete Leute die damit verbundenen Anliegen verstehen konnten. Ich stimme dieser kunsthistorischen Einbettung deshalb nicht zu, weil Leonardo seine Botschaft offenkundig verschlüsselt, sodaß sie eigentlich nur ein ebenbürtiges "Genie" entziffern kann; und das ist, in der Tat, die große Leistung der Autoren.
Um Leonardos Idee nachvollziehen zu können, muß man beachten, daß die Zeichnung zwei deutlich markierte Punkte auf der Brust-Linie enthält, die keine geometrische Beziehung zu anderen Details der Zeichnung zu haben scheinen. Andererseits findet man die Punkte, wo die Enden der Glieder das gegebene Quadrat und den Kreis berühren, dadurch betont, daß es sich nur um die Spitze eines Fingers, des Mitelfingers, handelt. Der Nabel als Zentrum dieses Kreises ist ein weiteres sichtbares Element dieses Arrangements; fügt man aber unsichtbare Elemente hinzu, dann offenbart sich deutlich die geometrische Funktion der anderen Punkte auf der Brustlinie.
Der erste Schritt dieses Prozesses ist eine Unterscheidung
zwischen dem sichtbaren Quadrat (Q1, S. 105) und dem größeren
Kreis (K2) der Zeichnung. Offensichtlich ist ihre Beziehung nicht
durch eine Annäherung beider Fächen beeinflußt,
aber das Verhältnis zwischen beiden ist auch bis heute noch
nie berechnet worden: Bei einer Seitenlänge des Quadrats
mit der Einheit 1 beträgt es 1,61 ...
Fügt
man nun - in einem zweiten Schritt - einen kleineren (unsichtbaren)
Kreis (K1, S. 105) hinzu, der durch die in den Mittelfingern
betonten Berührungspunkte auf dem Quadrat angedeutet ist
und denselben Mittelpunkt im Nabel des Mann hat wie der sichtbare
große Kreis, dann errechnet man schon eine wesentlich bessere
Annäherung der Fläche des sichtbaren Quadrates mit
dem Wert von 1,1592446 (S. 98).
Interpretiert
man nun - in einem dritten Schritt - die beiden symmetrisch
auf der Brustlinie plazierten Punkte als Mittelpunkte zweier
Armbewegungskreise (r = x) (wie etwa beim Codex Huygens, Fol.
7, S. 88), dann kann die Brust-Linie in der Höhe h in die
drei Teile x + d + x aufgeteilt werden (S. 107).
In
einem vierten Schritt zieht man nun beide Kreise mit dem
Radius x um die markierten Punkte auf der Brust-Linie als ihre
Mittelpunkte: beide Kreise berühren offensichtlich die sichtbaren
markanten Elemente der Zeichnung: Die Spitzen der Mittelfinger
auf dem gegebenen Quadrat (Q1) und auf dem gegebenen Kreis (K2;
S. 108).
In einem fünften Schritt betrachtet man nun die Spannweite
der Beine (60°). Zieht man die Seiten dieses angedeuteten
Dreiecks über den Nabelpunkt hinaus bis zum Schnittpunkt
hk des gegebenen Kreises (K2), dann bekommt man ein geometrisches
Ensemble, das ein neues Quadrat mit hoher Flächenannäherung
an den sichtbaren Kreis (K2; S. 109) erzeugen kann.
Das
bedeutet - in einem letzten Schritt - nur noch die horizontale
Linie durch die Schnittpunkte hk des vorhandenen Kreises (K2)
nach beiden Seiten zu verlängern, bis die Länge mit
der Höhe h identisch ist, und man gewinnt ein neues Quadrat
(Q2; S. 110). Das Verhältnis zwischen diesem rekonstruierten
unsichtbaren Quadrat und dem sichtbaren gegebenen Kreis beträgt
0,999, wenn man das vorhandene Verhältnis zwischen dem sichtbaren
Quadrat (Q1) und dem sichtbaren Kreis (K2) mit 1,61 ... zugrunde
legt.
Nimmt man (wie wahrscheinlich Leonardo)
an, daß bereits zwischen dem sichtbaren Q1 und dem unsichtbaren
K1 eine Gleichflächigkeit besteht, dann berechnet sich das
Verhältnis von dem sichtbaren K2 zum konstruierten (unsichtbaren)
Q2 mit dem Wert 1,0004112.
Dieser Prozeß
der Erzeugung eines neuen Quadrates und Kreises kann auf der
Grundlage der vorherigen wiederholt werden. Die Annäherung
der Flächen wächst Schritt für Schritt auf den
Grenzwert von 1,000373 zu. Toleriert man diese Differenz - in
den Augen Leonardos "nur ein Punkt" - dann ist dieses
Modell eine rein geometrische Methode der Kreisquadratur.
Wir wissen heute, daß K.F.Gauß später bewiesen
hat, daß eine exakte Kreisquadratur mit Zirkel und Lineal
mathematisch unmöglich ist, aber auf dem Hintergrund des
antiken Wissens ist Leonardos Vorgehensweise eine originäre
Erfindung und beweist seinen mathematischen Genius ebenso wie
die theoretische Einbildungskraft der Verfasser Schröer
und Irle, die seine versteckte Botschaft entschlüsseln konnten.
Gert
Sperling, *21.06-44, studierte Ev. Theologie und Alte Sprachen
an der Kirchlichen Hochschule in Bethel und Theologie und Sozialwissenschaften
an der Philipps-Universitat Marburg. Nach zwei Jahren Lektorat
an der Universitat wurde er Vikar an der Elisabethkirche in Marburg
und ab 1976 Studienassistent am Predigerseminar in Hofgeismar.
Seit 1976 Durchfuhrung von Studienfahrten in in Europa mit Schwerpunkt
Rom. Er ist Pfarrer in Fuldatal-Ihringshausen, Rundfunksprecher
der Landeskirche von Kurhessen-W. und theologischer Studienleiter
in Kassel-Land. Er hat auf der Grundlage einer neuen Vermessung
vo 1989 eine interdisziplinare Studie zum Pantheon verfasst:
Das Pantheon in Rom: Abbild und Mass des Kosmos (Neuried: Ars
una Verlagsgesellschaft mbH, 1999).
RELATED SITES ON THE
WORLD WIDE WEB
DIESES BUCH
"Ich aber quadriere den Kreis..." Homepage
Klaus Schröer's HomepageLEONARDO DA VINCI
Biography of Leonardo da Vinci
A Man of Both Worlds
Da Vinci: Scientist, Inventor, Artist
Vinci: Leonardo's Home TownSQUARING THE CIRCLE AND PI
Squaring the Circle
Squaring the Circle: Hobbes on Philosophy and Geometry
Squaring the circle using a special kind of polygon
The Number Pi


Copyright ©2000 Kim Williams Books