Klaus Schröer and Klaus Irle . "Ich aber quadriere den Kreis..." (Münster: Waxmann Verlag, 1998). To order this book from Amazon.de, click here!

The title of this German-language book, "Ich aber quadriere den Kreis...", is a quote from Leonardo da Vinci himself (Windsor 12280 r, 1508-9; p. 37), in which he remarks that Archimedes "squares a polygon, but not the shape of a circle" ("adunque archimenjde non quadra maj figura di lato curvo"; p.18). Leonardo emphasizes his aim to square really curved figures. Authors Klaus Schröer and Klaus Irle refer to several sources where Leonardo expresses his conviction that he is able to develop a method to accomplish this using straightedge and compass in a purely geometrical manner: the reconstruction of the authors demonstrates that in the end of the geometrical process we find the good approximation of 1.000373 between the shape of the circle and the square with a side-length of the unit 1. But there is no comment or explanation in Leonardo's manuscripts about mathematics, geometry and art-theory concerning this claim; only some other experiments with circular and spherical sections and various notes about the squaring of a circle are mentioned.

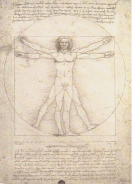
The book is a teamwork of an art-historian (Dr. Klaus Irle) and an artist using mathematics (Klaus Schröer). They prove that over the course of 500 years the famous and well-known drawing of the so-called "Vitruvian Man" by Leonardo has been viewed as a Renaissance interpretation of human proportions according to the rules and measures of Vitruvius, but that there was no perception of the mathematical fact that in these human proportions Leonardo has identified a purely geometrical concept of the "squaring of the circle". But this "hidden story" of the drawing is (perhaps intentionally) encoded, and has not been detected throughtout the last five centuries of art history for two main reasons:

1) The art history of the past two centuries ignored the intimate relationship between mathematics and art in the Renaissance based on the recognition of ancient knowledge (Panowsky, 1940; Ost, 1975; Kemp, 1981; Zöllner, 1987; Braunfels Esche, 1994; p.67 ff.).
2) The art of the last two centuries is defined by emphasizing the feelings and subjective perception of the artist and is not determined by everlasting mathematical rules, frames and laws in order to create an image of the "objective" reality.

In an attempt to rectify this situation, the authors revitalize the Renaissance aspects of art theory, especially as regards the art of painting and its relationship to mathematics. Leonardo, called an "Universal Genius", was an all-round scientist in "mathematics, anatomy, mechanics, hydraulics, geology, astronomy, zoology, botany and the rules of painting" (p.13) and the full spectrum of his work fills libraries in Milan, Turin, Rome, Paris, London, Oxford, Madrid, New York and Los Angeles. His hydraulic studies are completely the private property of Bill Gates (Microsoft). In the gathered codices we find many remarks by Leonardo regarding mathematical trials (including the squaring of the circle), but the study of the "Vitruvian Man" is not interpreted in this mathematical context of one of the most famous ancient "mathematical riddles".

To understand this "work of rules" it is necessary to compare the text version of Vitruvius and the content of Leonardo's drawing, because there are three important differences:
1) Leonardo spreads up the legs of the man to exactly 1/14 of its height. The text of Vitruvius is without any calculation.
2) According to Leonardo, the arms have to be lifted up to the top of the head, so that the fingertips are touching this (head-)line. There is no remark by Vitruvius.
3) By this position of the limbs, the span of the spread legs is an isosceles triangle. We find no comment by Vitruvius.

There are also differences between the fractions of distances between Vitruvius and Leonardo: Leonardo gives the upper breast-line as the sixth part of the body height, Vitruvius calculates 1/6 + 1/40. Vitruvius measures the body height as 6 feet, while Leonardo measures it as 7 feet. This means that Leonardo has created a new proportional study in relation to the ancient one of Vitruvius. As a consequence of this modification, it is possible to integrate a geometrical process of squaring the circle (high approximated).

In my opinion Leonardo demonstrates that he has surpassed Vitruvius by setting Vitruvius' text to a certain extent "behind" his own drawing; the drawingn edges it out so that the circle seems to cover the ancient text, while Leonardo's own text shows something like a headline and is clearly marked off from the drawing by the line indicating units of measurement (see figure above). The authors want to identify this combination of text and picture in the tradition of the so-called "emblematic art" in the 15th to the 17th century, a kind of small-format literature with a headline (Vitruvius), a picture (the drawing) and the comment on the picture (Leonardo's text). But this genre was originally created to show the value of moral laws and ethics or matters of life philosophy in an elementary way, so that uneducated people were also able to understand it. I do not agree with this interpretation, because it appears to me that Leonardo is "coding" his message, so that only another "genius" can decipher it; and this, indeed, is the great achievement of the authors.

In order to follow Leonardo's idea, one has to pay attention on the fact that there are two marked points on the breast-line, which seem to have no geometrical relationship to other details of the design. On the other hand, one can recognize that the points where the tops of the limbs are touching the given square and circle are evidently emphasized by the tip of only one finger, the middle-finger. The navel, as center of the circle, is another visible element of the arrangement; invisible elements have to be added to reveal the geometrical function of the other points on the breast-line.

The first step of the process is the distinction between the given visible square (Q1, p.105) and the greater circle (K2) of the design. Evidently their relationships are not influenced by an approximation of their shapes, but the proportion is not calculated yet: Giving the side of the square the unit 1, the proportion is 1,61... .
If, in a second step, a smaller (invisible) circle (K1, p. 105) is added now (indicated by the emphasized points of the middle fingers on the square with the same centerpoint (the navel), then there is calculated a better approximation to the shape of the visible square with a value of 1,1592446 (p. 98).
Now, in a third step, the two symmetrically arranged points on the breast-line are interpreted as center-points of two axial circles of the moving arms (r = x) (relationship to Codex Huygens, Fol. 7, p. 88). In the consequence of this, the breast-line on the height h is divided in three parts x + d + x (p. 107).
In a fourth step, these circles with the radius x are drawn with both visible points of the breast-line as their centerpoints: they evidently touch both visible elements of the design: the tops of the middle fingers on the given square (Q1) and on the given circle (K2; p. 108).
In a fifth step you have to take the span of the legs into consideration (60°). If the sides of this indicated triangle are extended through the navel to the intersection point hk of the given circle (K2), you have a new geometrical ensemble, able to create a new square with a high approximation to the given circle (K2; p. 109).
That leads to a last step: The extension of the line through the cutting points hk to the length of their height generates a new square (Q2; p. 110). The proportion between this invisible reconstructed square and the given visible circle is 0,999, taking the proportion between the visible square (Q1) and circle (K2) with 1,61.
Assuming (like Leonardo) a total equality of the visible Q1 and the invisible K1, then the calculation of the proportion K2 (visible) : Q2 (invisible) has the value of 1,0004112.

The process of generating a new square and circle can be repeated on the base of the reconstructed new forms. The approximation of their shapes goes up step by step to the borderline value of 1,000373. Tolerating this difference of - in the eyes of Leonardo - "only a point", this method is a purely geometrical system of squaring the circle. We know, that later on K. F. Gauß demonstrated the impossibility of an exact squaring of the circle with straightedge and compass, but on the basis of the ancient knowledge, the procedure of Leonardo is an orginal new invention and proves his mathematical genius, as well as the powers of imagination of authors Schröer and Irle.

THIS BOOK
"Ich aber quadriere den Kreis..." Homepage
Klaus Schröer's Homepage

LEONARDO DA VINCI
Biography of Leonardo da Vinci
A Man of Both Worlds
Da Vinci: Scientist, Inventor, Artist
Vinci: Leonardo's Home Town

SQUARING THE CIRCLE AND PI
Squaring the Circle
Squaring the Circle: Hobbes on Philosophy and Geometry
Squaring the circle using a special kind of polygon
The Number Pi

ABOUT THE REVIEWER

Gert Sperling studied ancient languages and evangelical theology at the Kirchlichen Hochschule in Bethel/Bielefeld, and Theology and Social Sciences at Philipps-Universität, Marburg. He taught for two years at the University before becoming vicar at Elisabethkirche. He was assistant director of studies for the formation of ministers at the Ev. Predigerseminar, Hofgeismar. Since 1976 he has led study tours of Europe, with a special emphasis on Rome. He is Minister in Fuldatal Ihringshausen and is a radio commentator for the Landeskirche of Kurhessen-Waldeck. He has been studying the Pantheon since 1989, and is the author of a newly-released book, Das Pantheon in Rom: Abbild und Maß des Kosmos (Neuried: Ars Una Verlagsgesellschaft mbH, 1999).

Copyright ©2000 Kim Williams Books