
|
Palladio's Villa Emo: The Golden Proportion Hypothesis Rebutted |
|---|
Professor of Design and Computation
Center for Medieval and Renaissance Studies
University of California
Los Angeles CA 90095-1615 USA
Not all that tempts your wand'ring eyes
And heedless hearts, is lawful prize;
Nor all that glisters, gold
Thomas Gray, 'Ode on the Death of a Favourite Cat'
HISTORICAL GROUNDING
In a most thoughtful and
persuasive paper [Fletcher 2000], Rachel Fletcher comes close
to convincing that Palladio may well have made use of the 'golden
section', or extreme and mean ratio, in the design of the Villa
Emo at Fanzolo which was probably conceived and built during
the decade 1555-1565. It is early in this period, 1556, that
I dieci libri dell'archittetura di M. Vitruvio Pollionis traduitti
et commentati ... by Daniele Barbaro was published by Francesco
Marcolini in Venice and the collaboration of Palladio acknowledged.
In the later Latin edition [Barbaro 1567], there are geometrical
diagrams of the equilateral triangle, square and hexagon which
evoke ratios involving ![]() and
and ![]() , but there are
no drawings of pentagons, or decagons, which might explicitly
alert the perceptive reader to the extreme and mean proportion,
, but there are
no drawings of pentagons, or decagons, which might explicitly
alert the perceptive reader to the extreme and mean proportion,
Architectural examples employing 2 and 3 include the Roman theater and Greek theater, respectively. A figure designed to illustrate Vitruvius's written description of a peripeteral circular temple shows one with columns spaced at 20 equal points around a circumference. Another figure shows arrangements for tetrastyle and hexastyle porticoes and, here following Vitruvius, a 20-gon sets out the position of the flutes around a column's cross-section. In both these examples, a pentagon, or decagon, will have been used in the geometric construction. Elsewhere, a pentagonal bastion is illustrated, but this plan is definitely not based on an equilateral pentagon.
In the archaeological Book IV of I quattro libri dell'archittetura, published by Domenico di Franceschi in Venice in 1570 [Eng. trans. Palladio 1997], Palladio illustrates the circular, twenty-columned Temple of Vesta and the decagonal-based Temple of Minerva Medica. In Book I, a Doric column displays the 20 flutes prescribed by Vitruvius.[1] The most telling use of the pentagon occurs as a minor detail in two inventioni for architraves surrounding doors and windows - but more of this later.
How would Barbaro—and perhaps his illustrator, Palladio—have constructed a pentagon or decagon? In the mid-fifteenth century, Alberti had described in words an exact construction for the decagon.[2] Albrecht Dürer, 1525, illustrates two distinct constructions for the pentagon, one according to geometric theory, and another traditionally used by masons and craftsmen which is only approximate [Dürer 1977: 144-147]. By the 1540s, Serlio shows Dürer's exact construction [Serlio 1996: 29]; yet as late as 1569, Barbaro shows only Dürer's approximate construction [Barbaro 1569: 27]. Whereas the exact construction leads to the extreme and mean ratio, the approximate construction does not. Someone seriously aware of the relationship of the extreme and mean ratio to the pentagon, or decagon, would surely use the exact method, especially if that relationship was seen to have aesthetic value. But there really is no evidence that any of these authors had strong commitments to the extreme and mean ratio for aesthetic purposes.
While Luca Pacioli enthuses over the extreme
and mean ratio in the first book of De divina proportione,
published by Paganius Paganinus in Venice in 1509, he does so
to make a theological point: that the properties of the ratio
may be likened to the Godhead in certain respects. In the second
book of the text, Pacioli summarizes his knowledge of architectural
practice, but he makes no connection between this Vitruvian precis
and his paean for divine proportion. It is Kepler in the seventeenth
century who connects the extreme and mean ratio with natural
phenomena such as planetary motion, and makes the discovery that
successive pairs in the sequence 1, 2, 3, 5, 8, 13,.... converge
on the value of the extreme and mean ratio—without in anyway
relating this to the sequence which occurs in a problem solved
by Fibonacci in the thirteenth century and had laid dormant until
its rediscovery in the nineteenth [Herz-Fischler 1987: 159-160].
The extreme and mean ratio emerges, born again as the 'golden
section', as a key to aesthetic measure only in the nineteenth
and twentieth centuries. Over the last century and a half, its
aesthetic use has been sanctioned, even sanctified, by casting
its diagrammatic aura over the analysis of past works in the
arts from architecture, to painting and sculpture, to music and
poetry; and by observing its pervasive presence in nature, in
growth patterns, or phyllotaxis.[3] None of this will be found in Renaissance
commentaries. None.
PALLADIO UNGILDED
It is true that the Fibonacci ratios 1:1,
2:1, 3:2, 5:3, 8:5, 13:8 will be found in Palladio's works, but
they represent less than six per cent of all ninety ratios to
be found in Book II nor do they occur as a coherent set in any,
but one, work [March 1998: 278, Appendix II, Table 2]. Except
for 13:8, the remaining five ratios have a musical interpretation
within the contemporary senario of the music theorist Gioseffo
Zarlino.[4]
Indeed, the ratio 13:8 produces a pitch which is very much out
of tune with the modern major and minor scales then beginning
to displace the traditional modes, and ![]() is yet more cacophonic and utterly disharmonious in musical theory
and to the ears.
is yet more cacophonic and utterly disharmonious in musical theory
and to the ears.
The one errant work is the Villa Mocenigo at Marocco, built at the same time as Villa Emo, but since destroyed [Palladio 1997: 55]. It has four 13:8 rooms, four 8:5 rooms. It also has four, square rooms and a square atrium with four columns, 1:1. The atrium is part of a large double square space, 2:1, containing the grand stairs. The remaining part of this double square space, between the entrance loggia and the stairs, is proportioned 8:5. Palladio ranges the lengths of two rooms, 10 piedi [5] and 16 piedi, against a single room 26 piedi long. Ignoring, as he seems to do, wall thickness, he uses the simple additive relation 10 + 16 = 26. In classical arithmetic, the arithmetic of the quadrivium, 16 is recognized as the Nicomachus X (tenth) mean of the extremes 10 and 26 [Nicomachus 1938: 284], and not as the second term in the then unrecognized additive relation of a Fibonacci sequence.
Palladio does use ratios which better converge
towards the finitely unreachable extreme and mean ratio. These
lie between the underestimate 8:5 ![]() and the overestimate 5:3
and the overestimate 5:3 ![]() .
The ratio 13:8 (=1.625) is among these, but 21:13
.
The ratio 13:8 (=1.625) is among these, but 21:13 ![]() is
not one of them.
is
not one of them.
Palladio uses the dimensions 26 ½ piedi to 16 for principal rooms in three different works: the Villa Badoer [Palladio 1997: Book II, 48], Villa Cornaro [Palladio 1997: Book II, 53], and Villa Saraceno [Palladio 1997: Book II, 56]. The ratio is 53:32 (=1.65625), which derives from the Nicomachus X sequence:
In a project for Count Barbarano [Palladio 1997: Book II, 22], the vaulted entrance has dimensions 41 ½ by 25 piedi, or a ratio of 83:50 (=1.66) from the sequence:
In his reconstruction of a private house for the ancient Romans [Palladio 1997: Book II, 35], the atrium is shown with dimensions 83 1/3 by 50 piedi. Adding the additional one third of a piede over the previously mentioned scheme turns this into the ratio 5:3. Of this ratio, Palladio writes: "I like very much those rooms which are two-thirds longer than their breadth" [Palladio 1997: Book I, 55 and 60].
The ratio 28:17 (H1.647) is found in the two largest rooms in the Palazzo Antonini [Palladio 1997: Book II, 5]. The ratios of consecutive terms in the Nicomachus X sequence converge, as do all such ratios, on the extreme and mean ratio in the long run:
In a previous analysis [March 1998: 236-239], it has been suggested that the proportional design of this building is an occult play on Plato's Timaean theme of world-making elements: the equilateral triangle related to the faces of the tetrahedron (fire), the octahedron (air), and the icosahedron (water); the square related to the faces of the cube (earth); and the equilateral pentagon to the faces of the decahedron (cosmos). The large rooms are proportioned by the equilateral pentagon : the width to the side, 17 piedi, and the length to the chord, 28 piedi. The side to chord were known to be in the extreme and mean ratio from contemporary readings of Euclid. This knowledge had been central to Piero della Francesca's innovative programme to arithmeticize geometry in the fifteenth century, in particular, the geometry of the Platonic solids [Davis 1977].
The rooms that lie behind these great rooms
are proportioned quadrato, or where "the length will equal
the diagonal of the square". The ground-floor hall is 32
piedi long and 28 piedi wide: a ratio of 8:7. This
is the ad triangulum ratio used in determining the dimensions
for the elevation of Milan Cathedral in 1392 [Ackerman 1949;
Ackerman 1991]. On a base of 8 units, the height of an equilateral
triangle is close to 7 units. In other words, 8:7 is a rational
convergent to ![]() (Figure 1).
(Figure 1).
To arrive at such proportional design, it
seems that Palladio would have made use of rational estimates
for square roots of non-square numbers, such as 2, 3 and 5. There
were several techniques for computing the numerical values at
the time, but once such computations were made it would probably
have been convenient to look them up in tables, or simply to
remember at least the most commonly used values. Typical values
in the generative process which converge on these square roots
are given in Table 1.[6]
Note that the ratio 5:3 may stand for ![]() ,
and is not to be read uniquely as an early term in a Fibonacci
approximation to
,
and is not to be read uniquely as an early term in a Fibonacci
approximation to ![]() .
.
|
Recall that the Fibonacci sequence was unknown as such during the Renaissance, and was most probably burrowed away as the solution to the rabbit breeding problem in some dusty, unstudied manuscript. How then do the numbers, 89, 144, 233, from the sequence
arrive, as a handwritten note, on a copy
of a 1509 edition of Euclid by Luca Pacioli [Herz-Fischler 1987:
157-158]? The value of ![]() was
certainly known from Euclid as
was
certainly known from Euclid as ![]() .[7] Substituting
the rational convergents for
.[7] Substituting
the rational convergents for ![]() ,
shown in Table 1, into this formula gives the answers set out
in Table 2. It will be noted that the first row gives the usual
Fibonacci sequence, F(2), but the second row gives ratios from
the sequence
,
shown in Table 1, into this formula gives the answers set out
in Table 2. It will be noted that the first row gives the usual
Fibonacci sequence, F(2), but the second row gives ratios from
the sequence
Table 2.Values of |
Earlier, the discussion of pentagonal proportional design in two inventioni by Palladio was postponed. With Tables 1 and 2 at hand, it is now possible to proceed. The designs are for door and window architraves. Palladio illustrates how to set out the gola diritta, an S-shaped moulding in the cornice [Palladio 1997: Book I, 57]. Palladio describes the construction of this curve:
To make it well and gracefully, draw a straight line AB and divide it into two equal parts at the point C; divide one of these halves into seven parts and make six of these coincide at point D; then one forms two triangles AEC and CBF; and at the points E and F fix the compass and draw the segments of a circle AC and CN which form the gola (Figure 2).
This construction is no whim. It derives from an arithmetical interpretation of Euclid, Proposition 10, Book XIII [Heath 1956: 455-457]. Unquestionably to be counted among the most aesthetically pleasing of all the propositions in The Elements, Proposition 10 reads: "If an equilateral pentagon be inscribed in a circle, the square on the side of the pentagon is equal to the squares on the side of the hexagon and on that of the decagon inscribed in the same circle" (Figure 3).
Let the side of the pentagon be s,
and the radius of the common circle be r (Figure
4). The side of the hexagon
is equal to the radius, and the side of the decagon is in proportion
to the radius as ![]() . In
modern terms, Proposition 10 may be expressed algebraically as:
. In
modern terms, Proposition 10 may be expressed algebraically as:
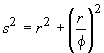
whence, the side of the pentagon
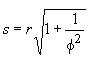 .
.Using the defining relation
and the value
the expression for the side can be reduced to
Computationally, this is what Euclid's proposition
implies; and, without the advantages of modern algebraic notation,
this is very much the kind of procedure that Piero della Francesca
would have had to follow in his fifteenth-century programme for
the arithmeticization of Euclidean geometry. How would such an
expression, albeit in different notation, be evaluated? It would
be necessary to substitute a rational value for ![]() .
But what value? It would be convenient if the remaining square
root after the substitution was of a square, or near-square,
number. Scanning through Table 1, the values 9/4 and 20/9 show
promise since the numerators are square numbers and their roots
can be brought outside the main square root sign. The value 9/4
leads to
.
But what value? It would be convenient if the remaining square
root after the substitution was of a square, or near-square,
number. Scanning through Table 1, the values 9/4 and 20/9 show
promise since the numerators are square numbers and their roots
can be brought outside the main square root sign. The value 9/4
leads to
but 22 is not a near-square number, whereas the value 20/9 gives
and ![]() is very close to
is very close to ![]() . Thus,
a good rational solution is
. Thus,
a good rational solution is
(Figure 5).
This is precisely the ratio that Palladio employs in his triangles AEC and CBE. Now, each is seen to be the isosceles triangle on the side of an equilateral pentagon with apex at the center of the circumscribing circle. Referring to Table 2, it will be found that an equilateral pentagon of side 3.7 = 21, will have a chord length of 34, and proportionately will have a radius of 3.6 = 18. This example is typical of the wit required to find integral values to fit the numerical irrationality of most geometrical objects, especially before the arrival of decimal notation in the seventeenth century (Figure 6).
The value 20/9 used here to arrive at Palladio's
construction, gives added credence to the interpretation that
the 20 x 9 rooms in Villa Barbaro at Maser were designed conceptually
to the ratio ![]() , or
the diagonal of a double square to its width [March 1998: 267-271].
Table 3 summarizes the proportional design at Maser.
, or
the diagonal of a double square to its width [March 1998: 267-271].
Table 3 summarizes the proportional design at Maser.
Table 3. Column 1: dimensions of rooms in the casa domenicale of Villa Barbaro at Maser, including the 14x12 vaulted crossing. Column 2: rational ratios. Column 3: root equivalents from Table 1. Root-4=2 and Root-1=1 are shown to enhance the underlying pattern. |
The rooms and spaces now are seen to be a play on the theme of the Pythagorean 3-4-5 triangle, but using root forms that Alberti had advocated in the 1450s.[8] The appearance of the ratio 7:6 here finds a different interpretation from the previous pentagonal one. Now it is seen as the base of an equilateral triangle to its height—a relationship that allows for the proportional design of the Star of David to be placed at the crossing, without, it should be noted, even the faintest whiff of today's political connotations (Figure 7).
FITTING A CLOAK OF GOLD
Rachel Fletcher takes drawings
of Villa Emo and overlays these with regulating lines. In doing
so she follows a time honored analytical methodology. Her overlays
show very clearly that the proportional design of the Villa may
have been generated by applying the golden ratio consistently
throughout. There is no doubt concerning the hypothesis: "Golden
Mean proportions appear in the Villa Emo, whose measured drawings
suggest that Palladio employed mathematical proportions through
a consistent application of geometric techniques" [Fletcher
2000: 78] (Figure 8).
Essentially, the analysis plays on the well-known property that when either a square is added to the short side of a golden rectangle, or a square is deducted from a golden rectangle, the new issue is itself a golden rectangle (Figure 9).[9] The golden rectangle itself may be generated from the square by striking a circular arc from the center of a side through an opposite corner (Figure 10). Following this method, the composition of the Villa Emo is generated from an initial square (Figure 11).
MISFIT
The method replicates the golden
proportional scheme with which Rachel Fletcher cloaks Villa Emo.
How well does this cloak fit? Visually, it looks fine, but suppose
a check is made with the dimensions that Palladio shows on his
own woodcut of the project (Figure
12)?
A simple model that compares Rachel Fletcher's analysis with Palladio's declared dimensions can be established with two unknowns: x the wall thickness, and y the expected value of Æ, the golden section (Figure13).
If the wall thickness is an unknown x, and an as yet undetermined continuous proportion is assumed for the design 1: y :: y : y2, then the proportion
must hold. This requires that the equation
be true. The equation reduces to the parabola
Set x = 1, that is, assume a unit wall thickness. The equation then becomes
The solutions to this are ![]() and
and ![]() .
.
These values do not correspond to the hypothesis
that ![]() , the golden section.
The first value falls short of the golden section value of 1.618...
by almost 12%. The second solution is too way out even to contend.
, the golden section.
The first value falls short of the golden section value of 1.618...
by almost 12%. The second solution is too way out even to contend.
Suppose that the wall thickness is larger. Set x = 2 as a trial. The equation is then
This is worse than the previous result, and since the function is monotonic, any increase of wall thickness beyond 1 piede will never make things better.
Try the assumption that Palladio has used centerline dimensions. Set x = 0.
The solutions to this are ![]() and
and
![]() . These are still
totally inadequate estimates for
. These are still
totally inadequate estimates for ![]() .
.
What values of x, the wall thickness,
will deliver the accepted value of ![]() ?
Take the original equation
?
Take the original equation
and set ![]() .
The equation now reduces to the linear equation
.
The equation now reduces to the linear equation
The solution gives ![]() ,
or a negative wall thickness of over 5 piedi! The computations
may be illustrated graphically (Figure
14 and Figure
15).
,
or a negative wall thickness of over 5 piedi! The computations
may be illustrated graphically (Figure
14 and Figure
15).
CHAMBER MUSIC...
The number set for Villa Emo [Palladio
1997: Book II, 55] comes from the distinct dimensions shown in
the plan,
The subset,
![]() ,
numerals on lines sloping to the left are multiples of 2, those
to the right of 3. The complete lambda is replete with arithmetic,
geometric and harmonic means. In the figure, the lambda is only
extended to the extreme values of the Villa Emo subset (Figure 16).
,
numerals on lines sloping to the left are multiples of 2, those
to the right of 3. The complete lambda is replete with arithmetic,
geometric and harmonic means. In the figure, the lambda is only
extended to the extreme values of the Villa Emo subset (Figure 16).
The set is rich in classical proportionalities:[10]
|
|
|
|
|
|
|
|
|
|
|
|
are geometric proportionalities in which the ratio of the difference between the greater extreme and the mean and the difference between the mean and the lesser extreme to is equal to the ratio between the mean and the lesser extreme. The proportionality
is arithmetic in which the difference between the mean and the lesser extreme is equal to the difference between the greater extreme and the mean.
There are two harmonic proportionalities in which the ratio of the difference between the greater extreme and the mean to the difference between the mean and the lesser extreme is equal to the ratio of the two extremes,
|
|
|
|
|
|
There is also one example of the Nicomachus X mean:
|
|
|
where the difference of the greater extreme and lesser extreme is equal to the mean. This will be recognized as being in proportion to the first three terms in what is now known as the Fibonacci sequence, F(3).
The full dimensional set for Villa Emo, E(2, 3, 5), can be arranged on a three-dimensional version of the lambda (Figure 17). Here, numerals lying on the vertical lines are multiples of 5. This new lattice holds all those numerals which may be factorized into products of 2, 3 and 5 (including their zero presence, in modern notation 203050 = 1). Whereas the first lambda is classical, this extended version is an example of a modular lattice in modern theory.
In addition to the proportionalities in the first lambda,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
are arithmetic proportionalities.
The proportionality
is harmonic. There are also five less familiar classical proportionalities in the full Villa Emo set, E(2, 3, 5). The proportionality
|
|
|
is Nicomachus IV, subcontrary to harmonic, in which the ratio of the difference between the greater extreme and the mean to the difference between the mean and the lesser mean is equal to the ratio of the lesser extreme to the greater. The proportionality
is Nicomachus VII in which the ratio of the difference of extremes, 16 - 12 = 4, to the difference of the first two terms, 15 - 12 = 3, is in the same ratio as the extreme terms, 4:3. The proportionality
is also a Nicomachus VII in which the ratio of the difference of extremes, 27 - 9 = 18, to the difference of the first two terms, 15 - 9 = 6, is in the same ratio as the extreme terms, 3:1. The proportionality
|
|
|
is Nicomachus X, which in modern terms comes from the Fibonacci sequence,
The proportionalities
|
|
|
|
|
|
are Nicomachus X, which corresponds to the Fibonacci sequence,
Finally, the proportionality
does not figure among Nicomachus's ten means, but is an instance of Pappus 8 [11] in which the difference of extremes, 20 - 15 = 5, to the difference of the last two terms, 20 - 16 = 4, is in the same ratio as the last terms, 20 : 16 :: 5 : 4.
Arithmetically, the Villa Emo set may be said to be rich in classical proportionalities. Such a set is the architect's proportional palette. He may not need all the colors, or even be aware of all the mixes, but Palladio, like his contemporary the music theorist Giosoffo Zarlino, undoubtedly appreciated the potentialities of a set based on the factors 2, 3, and 5. Its more recent architectural significance was investigated by Ezra Ehrenkrantz [1956] as a contribution to modular coordination for industrialized building.[12]
The Pythagorean lambda is the base for Plato's theory of universal
harmony. Pythagorean harmony is entirely based on a cycle of
perfect fifths, 3:2. From the unison, 1:1, the fifth 3:2, is
reached by ascending the scale. The fifth beyond this is 32:22
:: 9:4, and the fifth above this 33:23
:: 27:8. The pitch 2:3 is reached by descending the scale from
1:1. By bringing all these tones into one octave, from 1:1 to
2:1, the notes 1:1, 9:8, 4:3, 3:2, 27:16, 2:1 are established
to form a pentatonic mode. If the tonic, 1:1, is the note D,
then 9:8 will be E, 4:3 will be G, 3:2 will be A and 27:16 will
be B.
The principal room proportions in Villa Emo may be related to
these notes in the Pythagorean scale:
Table 4. Principal rooms in Villa Emo and their musical equivalent. |
On either side of the casa dominicale
at Villa Emo are the farm buildings. Here the room sizes are
48x20 (12:5), 20x12 (5:3) and 24x20 (6:5). The factor 5 is introduced.
These have a musical interpretation in Zarlino's, then very modern,
senario. The ratio 6:5 represents the minor third, and
5:3 the major sixth. The ratio 12:5 is an octave above 6:5. With
D as tonic, 6:5 would be F, 12:5 would be f', and 5:3 would be
B, displacing the sharper Pythagorean B, 27:16. These tones sit
comfortably in the heptatonic Dorian mode: DEFGABCd' . Villa
Emo is chamber music in the Dorian mode, in which the casa
dominicale uses the ancient Pythagorean scale, and the workaday
farm buildings in tune with the modern Zarlino scale—a hymn,
indeed, Ancient and Modern.
...OR A PATCHWORK OF PYTHAGOREAN TRIANGLES?
Buildings have to be
set out. Triangulation has been the method of surveyors since
time immemorial. Central to their work have been the rational
right triangles, the most celebrated of which is the so-called
Pythagorean 3-4-5 triangle. Three ropes, or rods, of these lengths
arranged in a triangle insure that the surveyor makes a right
angle [March 1998: 53-57 ('Right Triangular Number')].
Two triangles proportional to the 3-4-5 triangle, the first scaled
three times and the second scaled four times, provide five of
the ten dimensions in the Emo set. Three other dimensions are
derivable from these by simple doubling, or extension. The remaining
two dimensions are 2 piedi and 3 piedi for the
piers to the colonnade. These, too, can be derived with a little
more, but simple, manipulation (Figure
18).
The most direct application of the 3-4-5 triangle is in the 16 x 12 piedi rooms using the 12, 16, 20 version. This triangle 'fills' the room plan. The next most direct is the 16 x 16 piedi room in which the 12, 16, 20 version is rotated on its 16 piede side. The 27 x 16 piedi and 27 x 27 piedi rooms require the surveyor to use the 9, 12, 15 version of the 3-4-5 triangle, and to swing the rope of length 15 piedi around until it is aligned with the side of length 12 piedi, 15 + 12 = 27 piedi. It is that simple (Figure 19).
Look again at the Villa Emo, and look at the colonnade in front of the agricultural buildings (Figure 20). If a square of sides 12 x 12 piedi be constructed using the 9, 12, 15 version, then the diagonal of the square will be very close to 17 piedi.[13] Swinging a rope of this length perpendicular to the back wall of the colonnade marks the front edge of the piers. Now swinging the rope of length 15 in the same manner produces the 17 - 15 = 2 piedi depth to the pier and marks the back edge. The breadth of the piers is simply 12 - 9 = 3 piedi from the 9, 12, 15 triangle (Figure 21).
Using just five surveyor's ropes, of lengths 9, 12, 15, 16, 20 piedi, all ten dimensions shown in the plan of Villa Emo have been accounted for—directly, practically and without fanciful interpretation.
"NOT ALL THAT GLISTERS, GOLD"
The cat, Selima, in
Thomas Gray's ode "tumbled headlong in" a "tub
of gold fishes". Attracted by "the golden gleam",
she "stretched in vain to reach the prize". Selima
drowned, but lives on in Gray's celebrated ode and its warning:
"Not all that tempts your wand'ring eyes ... , is lawful
prize; Nor all that glisters, gold".
Villa Emo "glisters" among Palladio's works., but it is not cloaked in the gold of the golden proportion. If the cloak doesn't fit, you must acquit. Palladio is not guilty. But there is plenty of guilt to spread around. The author of the paper which "saw" the golden section in Villa Emo is an innocent adherent of a morphological church that has flourished since the advent of Zeising's work [1854]. But she is no Selima, that "Presumptious Maid!".
On the contrary, Rachel Fletcher has presented a diligent and exemplary study of its kind. Her misfortune, in casting a cloak of golden proportion over the Villa Emo, is that, unlike the quintessential studies of, say, M Borissavlievitch [1958], or R A Schwaller de Lubicz [1977], Palladio has given the actual measurements. In other studies, and in the absence of the architect's specification, the investigator is at liberty to choose where to take measurements and with what precision.: "With a little precision in taking measurements, it [the golden section] is easily found" [Schwaller de Lubicz 1977: 66]. But the cloak cannot be checked.[14]
What is surprising is that a visually gratifying result is so very wrong when tested by the numbers. It suggests that there is enormous opportunity for visual error in the search for the golden 'whatever', an error that computation exposes ruthlessly. Perhaps, the most alarming consequence of obedience to this morphological faith is that the extraordinary inventiveness, creativity, wit and playfulness of homo faber is analyzed into some ideal, universal system, post facto.[15] What is this overwhelming desire among some to trade Freedom for Necessity? The obsession with the golden section would be like musicians being fixed solely on the harmony of the common chord, ensuring that everything in their compositions was governed by its limiting proportion.
Palladio had no system of proportion. He was a mannerist. Rules were there to be challenged, to be transformed, to surprise in their unexpected application, or unforeseen consequence. In the process of design, as the dimensions of a work gather around the physical and geometric possibilities and constraints, the designer discerns familiar patterns and potential interpretations. For a humanist during the Renaissance, these might include Plato's Timaean myth, the classical orders of number taxonomy, Euclidean geometry, music theory, cosmology, or just plain, practical expediency. It can be assumed that Palladio's work is executed in a polysemic language, foreign to modern eyes: enrichingly ambiguous, despite its enticing presentational lucidity . Before Selima's eyes "betray'd a golden gleam", "She saw: and purr'd applause".
Look. Palladio cannot be seen through prescription glasses.
NOTES
[1] See Vitruvius [1999:
Book IV.3.9, 58]. Externally, it is to be noted that Palladio
does not use fluted columns in practice, denying himself - in
the Doric order - even a hint of the golden proportion. At significant
points in the interior, a few fluted Corinthian columns punctuate
the nave of San Giorgio Maggiore. return
to text
[2] Alberti gives a written description of the exact method for drawing an equilateral decagon. See [Alberti 1988: 196]. return to text
[3] See Thompson [1942: 912-933 ('On Leaf-Arrangement, or Phyllotaxis')]. Note particularly: "One irrational angle is as good as another: there is no special merit in any of them, not even in the ratio divina", p. 933. return to text
[4] 1:1, unison; 2:1, diapason; 3:2, diapente; 4:3, diatesseron; 5:3, major hexad; 8:5, minor hexad [Zarlino 1558] . Palesca [1985: 235-244] points out that Lodovico Fogliano (Musica Theoria, Venice, 1529) had already established the musical provenance of these ratios. return to text
[5] A piede (pl. piedi) is the Vicentine foot, equal to 0.357m. return to text
[6] See March [1998: 65-69 ('Inexpressible Proportion')]. return to text
[7] "If a straight line be cut in extreme and mean ratio, the square on the lesser segment added to half the square of the greater is five times the square on half of the greater segment" [Heath 1956, 3: Bk. XIII, Prop. 3, 445-447]. return to text
[8] Alberti [1988: 307] writes: "In establishing dimensions, there are certain natural relationships that cannot be defined as numbers, but that may be obtained through roots and powers". See [March 1999c]. return to text
[9] For a generalization of this, see [March 1999a] and [March 1999b]. return to text
[10] Nicomachus [1938: 264-284] enumerates ten proportionalities. H L Heath [1921, I: 84-89] summarises these results. See also [March 1998: 72-77 ('Proportionality')]. return to text
[11] Heath [1921, I: 87] shows that Nicomachus missed this additional mean, but that Pappus had recorded it as his eighth mean. return to text
[12] Note also Appendix 3 by F. St. J. Hetherton on the musical analogy, pp. 72-74. return to text
[14] Even when measurement can be replaced by plain counting, it may be unwise to implicate section d'or. O. A. W. Dilke [1987] asks: "is it only coincidence" that, in Polycletus's theater at Epidaurus (c350 BCE), the seats below and above the diazoma count 34 and 21 respectively to make 55 rows in all? He then relates this to the Fibonacci sequence and thence to the Golden Number. But there is a simple classical argument for this arrangement. 55 is the tenth trigonal number, and the decad is the root of all numbering. In classical Greek 55 is represented by en, whose pythmen is 5+5=10, and which spells the word One, the divine. The theater is located at a sanctuary and this dedication to the One is surely appropriate. The number 21 is the sixth trigonal number; but 6 is a perfect number, and so important to the ancient Greeks that it has its own non-alphabetical character - digamma. Setting out the decad 1, 2, 3, 4, 5, 6, and 7, 8, 9, 10, it will be seen that the sum is 55, the first six sum to 21, and the remaining trigonal gnomons count to 34. return to text
[15] "... all such speculations as these hark back
to a school of mystical idealism" [Thompson 1942: 933].
return to text
REFERENCES
Ackerman, James S. 1949. "Ars Sine Scienta Nihil
Est": Gothic Theory of Architecture at the Cathedral of
Milan. Art Bulletin 31: 211-263.
Ackerman, James S. 1991. Distance Points: Essays in Theory and Renaissance Art and Architecture. Cambridge MA: MIT Press. To order this book from Amazon.com, click here.
Alberti, Leon Battista. 1988. On the Art of Building in Ten Books. J Rykwert, N Leach, R Tavernor, trans. Cambridge MA: MIT Press. To order this book from Amazon.com, click here.
Barbaro, Daniele. 1567. M Vitrvvii Pollionis De Architectvra Libri Decem Cvm Commentariis. Venice: Francesco de Franceschi and Zuane Krugher.
Barbaro, Daniele. 1569. La Pratica della Perspettiva. Venice: Camillo and Rutilo Borominieri.
Borissavlievitch, M. 1958. The Golden Number: and the Scientific Aesthetics of Architecture. London: Alec Tiranti.
Cornford, F.M. 1952. Plato's Cosmology: the Timaeus of Plato with a running commentary. Rpt. 1997, Hacket Publishing Co. To order this book from Amazon.com, click here.
Davis, Margaret Daly. 1977. Piero della Francesca's Mathematical Treatises. Ravenna: Longo Editore.
Dilke, O.A.W. 1987. Mathematics and Measurement. Berkeley CA: University of California Press/British Museum. To order this book from Amazon.com, click here.
Dürer, Albrecht. 1977. The Painter's Manual. W.L. Strauss, trans. New York: Abaris Books.
Ehrenkrantz, Ezra D. 1956. The Modular Number Pattern. London: Alec Tiranti.
Fletcher, Rachel. 2000. Golden Proportions in a Great House: Palladio's Villa Emo. Pp. 73-85 in Nexus III: Architecture and Mathematics, K Williams, ed. Pisa: Pacini Editore. To order this book directly through the NNJ, click here. To order through Amazon.com, click here.
Heath, Thomas L. 1921. A History of Greek Mathematics. Rpt. 1981, New York: Dover. To order this book from Amazon.com, click here.
Heath, Thomas L., ed. 1956. The Thirteen Books of Euclid's Elements. New York: Dover. To order these books from Amazon.com, click here.
Herz-Fischler, Roger. 1987. A Mathematical History of Division in Extreme and Mean Ratio. Waterloo, Canada: Wilfred Laurier University Press. Republished as A Mathematical History of the Golden Number. New York: Dover, 1998. To order this book from Amazon.com, click here.
March, Lionel. 1998. Architectonics of Humanism: Essays on Number in Architecture. London: Academy Editions. To order this book from Amazon.com, click here.
March, Lionel. 1999a. Architectonics of proportion: a shape grammatical depiction of classical theory. Pp. 91-100 in Environment and Planing B: Planning and Design 26, 1.
March, Lionel. 1999b. Architectonics of proportion: historical and mathematical grounds. Pp. 447-454 in Environment and Planning B: Planning and Design 26, 3.
March, Lionel. 1999c. Proportional design in L B Alberti's Tempio Malatestiano, Rimini. Pp. 259-269 in Architectural Research Quarterly 3, 3.
Nicomachus of Gerasa. 1938. Introduction to Arithmetic. M.L. D'Ooge, trans. Ann Arbor MI: University of Michigan Press.
Palesca, Claude V. 1985. Humanism in Italian Musical Thought. New Haven CT: Yale University Press.
Palladio, Andrea. 1997. The Four Books of Architecture. R. Tavernor and R. Schofield, trans. Cambridge MA: MIT Press. To order this book from Amazon.com, click here.
Schwaller de Lubicz, R.A. 1977. The Temple in Man: Sacred Architecture and the Perfect Man. R. and D. Lawlor, trans. Rochester VT: Inner Traditions International. To order this book from Amazon.com, click here.
Serlio, Sebastiano. 1966. On Architecture. V. Hart and P. Hicks, trans. New Haven CT: Yale University Press.
Thompson, D'Arcy W. 1942. On Growth and Form. 2nd ed. Cambridge UK: Cambridge University Press.
Vitruvius. 1999. Ten Books on Architecture. Ingrid Rowland, trans. Cambridge UK: Cambridge University Press. To order this book from Amazon.com, click here.
Zarlino, Gioseffo. 1558. Le Istitioni harmonische. Venice.
Zeising, A. 1854. Neue Lehre von den Proportionen des menschlichen Körpers. Leipzig.
Andrea Palladio
Palladio's
Italian Villas
The
Palladio Museum
An
Itinerary of Villas and their Commissioners
Life of Palladio
The Golden Proportion
Rachel
Fletcher, "Golden Proportions in a Great House" (abstract,
Nexus 2000)
The
Golden Section in Art and Architecture
The
Golden Section Ratio: Phi
Proportion
and the Golden Ratio (Mathematics and the Liberal Arts)
ABOUT
THE AUTHOR
On the personal recommendation of Alan Turing, Lionel March was admitted
to Magdalene College, Cambridge, to read mathematics under Dennis
Babbage. There he gained a first class degree in mathematics
and architecture while taking an active part in Cambridge theater
life. In the early sixties, he was awarded an Harkness Fellowship
of the Commonwealth Fund at the Joint Center for Urban Studies,
Harvard University and Massachusetts Institute of Technology
under the directorships of Martin Meyerson and James Q Wilson.
He returned to Cambridge and joined Sir Leslie Martin and Sir
Colin Buchanan in preparing a plan for a national and government
center for Whitehall. He was the first Director of the Centre
for Land Use and Built Form Studies, now the Martin Centre for
Architectural and Urban Studies, Cambridge University. As founding
Chairman of the Board of the private computer-aided design company,
he and his colleagues were among the first contributors to the
'Cambridge Phenomenon' - the dissemination of Cambridge scholarship
into high-tech industries. In 1978, he was awarded the Doctor
of Science degree for mathematical and computational studies
related to contemporary architectural and urban problems.
Before coming to Los Angeles he was Rector and Vice-Provost of
the Royal College of Art, London. During his Rectorship he served
as a Governor of Imperial College of Science and Technology.
He has held full Professorships in Systems Engineering at the
University of Waterloo, Ontario; and in Design Technology at
The Open University, Milton Keynes. At The Open University, as
Chair, he doubled the faculty in Design and established the Centre
for Configurational Studies. He came to UCLA in 1984 as a Professor
in the Graduate School of Architecture and Urban Planning. He
was Chair of Architecture and Urban Design from 1985-91. He is
currently Professor in Design and Computation and a member of
the Center for Medieval and Renaissance Studies. He was a member
of UCLA's Council on Academic Personnel from 1993, and its Chair
for 1995/6. He is a General Editor of Cambridge Architectural
and Urban Studies, and Founding Editor of the journal Planning
and Design. The journal is one of four sections of Environment
and Planning, which stands at "the top of the citation
indexes." Among the books he has authored and edited are:
The Geometry of Environment, Urban Space and Structures,
The Architecture of Form, and R. M. Schindler: Composition
and Construction. His most recent research publications include:
"The smallest interesting world?", "Babbage's
miraculous computation revisited," "Rulebound unruliness,"
"Renaissance mathematics and architectural proportion in
Alberti's De re aedificatoria," and "Architectonics
of proportion: a shape grammatical depiction of classical theory."
His book Architectonics of Humanism: Essays on Number in Architecture
before The First Moderns, a companion volume to Rudolf Wittkower's
Architectural Principles in the Age of Humanism was published,
together with a new edition of the Wittkower, in the Fall 1998.
|
Lionel March, "Palladio's Villa Emo: The Golden Proportion Hypothesis Rebutted", Nexus Network Journal, vol. 3, no. 4 (Autumn 2001), http://www.nexusjournal.com/March.html |


Copyright ©2001 Kim Williams