
| A geometrical ensemble to generate the squaring of the circle |
|---|
Hauffstrasse 28
34125 Kassel, Germany
The purely geometrical squaring
of the circle with straightedge and compass is possible only
within the tolerance of an approximation. But knowing the value
of the irrational number pi of the circle (p = 3,14159265 ...), it is possible
to transform it as a line or rather as a shape
of a circle or a square. The number of the shape of a circle
is pr2
, the number of the shape of the square is (root-pr2 )2
= (r[root-p])2.
If the radius of the circle is r = 1, the shape of the
circle and the shape of the square DEFG equal p. In the following illustration
(Figure 1), the line of the unit is 5 cm. The square of
the unit therefore amounts 52 = 25 cm2.
The larger square NOPQ goes up to 22 = 4 units (or
102 = 100 cm2). This means that the shapes
of circle (= p)
and square (= p)
are smaller than this larger square.
The shape
of the square DEFG = p
observes the Pythagorean theorem a2 + b2
= c2 for right triangles, because the two shapes (square
DEFG and the surrounding shapes) add up to the square-shape NOPQ.
The formula is:
[5(root-p)]2 + [5(root-4 - p)]2 = 25 (p + 4 - p) = 100.
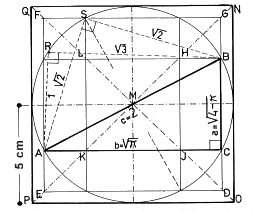
The inner circle of the larger square includes the right triangle:
The Pythagorean theorem confirms the equation ( 4 - p) + p = 4, and is also applicable to "irrational" right triangles. If you move the point C on its semi-circle between A and B, then there are demonstrated ad infinitum all possible right triangles. The sum of the squared catheti in every case equals 4 (for instance the triangle ABS: 2(root-2)2 = 4; the triangle ABR: 12 + (root-3)2 = 4), because all plane triangles are touching a revolving circle, their forms are represented in the picture of the squaring of the circle. It is a really "cosmological arrangement", because we are able to project the optical vaulted sky on to a planar celestial chart. On the other hand the circle with the radius 1 is the inner circle of a virtual right triangle with the sides 3:4:5. We have a given shape of the square in our design of 100, and in so far we could double this proportion 3:4:5 to 6:8:10 and integrate it into the circle: 62 + 82 = 102 (36 + 64 = 100).
Here we are able to identify a connection to the infinite
system of the so-called "primitive Pythagorean triples",
which include all natural and all positive real
numbers.
The many various imaginable triangles
in the circle like ABC can be put together (as a pair; two identical
axes) either to symmetrical rectangles or to deltoids (one identical
axis), if you superimpose the triangle ABC over the axis AB.
Rectangles and deltoids belong to the symmetrical polygons of
the circle. The shapes of the polygons, ACBR and ACBS for instance,
are nonsymmetrical. Two of the equal rectangles can be put together
(by rotation of 90°) to form the arms of a Greek Cross. Its
outer corners are the polygonal points of an inscribed symmetrical
octagon on the circle with the radius 1. Octagons have a centered
symmetry with eight axes. The shape of the inner square of the
cross HJKL equals the shape of the slim frame between NOPQ and
DEFG. In consequence of this, the shape with the value p is equal to
the shape of the larger frame between NOPQ and HJKL. This relationship
is valid in every case. Greek Crosses make it easier to make
out the relationships of many shapes and numbers within all plane
triangles, also between other polygons and concerning the squaring
of the circle. The most important aids (for the squaring of the
circle) are the Strahlensätze (intercept theorems)
and the evident Pythagorean theorem for right triangles. These
aids are valid with regards to all plane triangles, including
the famous irrational "Fermat triangles" (Pierre de
Fermat 1601 - 1665). This hypothesis provided geometrical explanations
in correspondence to the theory of numbers. A special case is
the centered symmetrical hexagon (Star of King David) with the
sides equal to 1, the most simple Fermat-equation 1n
+ 1n = 2 and the equilateral triangle, the so-called
"Eye of God".
Translated by Gert Sperling
REFERENCES
Schröer, Klaus and
Klaus Irle . "Ich aber quadriere den Kreis..." (Münster: Waxmann
Verlag, 1998). To order
this book from Amazon.de, click
here. Or, read the
Review
by Gert Sperling in
the NNJ, vol. 2 no. 1.
RELATED SITES ON THE WORLD WIDE WEB
Squaring the Circle
Squaring the Circle: Hobbes on Philosophy and Geometry
Squaring the circle using a special kind of polygon
The Number Pi
ABOUT THE AUTHOR
Dr.
Helmut Sander received his diploma in 1938, and studied architecture
from 1938 to 1945 at the TH Hannover. He is the technical director
of the state building authorities and the University of Kassell,
especially for the preservation of historic monuments. He worked
in particular on the "Herkules Monument" in Kassel-Wilhelmshoehe.
This building was the subject of his doctoral thesis at the University
of Berlin in 1981 (ISBN 3-87816-037-2). He has studied the theory
of numbers and geometry since 1948. He has published 25 papers
concerning Pythagorean theories in scientific periodicals.
|
Helmut Sander, "A Geometrical Ensemble to Generate the Squaring of the Circle", Nexus Network Journal, vol. 2 ( 2000), pp. 83-85. http://www.nexusjournal.com/Sander.html |
