4 Unified Field Theory and Quantum Mechanics

Obviously, Einstein did not trust an investigation like the experimental physicist Osborn’s (1917 – 2003) trying to show by ideal measurements that the notion of curvature can be applied only “in the large” where “the domain of largeness is fundamentally determined by the momentum of the test particle with which the curvature is measured” – due to limitations from quantum mechanics [465]. Osborn’s feeling obviously was shared by the majority of elementary particle physicists, in particular by F. Dyson:

Nevertheless, there were other physicists like Einstein for whom no divide between classical and quantum field existed, in principle.

4.1 The impact of Schrödinger’s and Dirac’s equations

In the introduction to Section 7 of Part I, a summary has been given of how Einstein’s hope that quantum mechanics could be included in a classical unified field theory was taken up by other researchers. A common motivation sprang from the concept of “matter wave” in the sense of a wave in configuration space as extracted from Schrödinger’s and Dirac’s equations. Henry Thomas Flint whom we briefly met in Section 7.1 of Part I, was one of those who wanted to incorporate quantum theory into a relativistic field theory for gravitation and electrodynamics. In Flint’s imagination, the content of quantum mechanics was greatly condensed: it already would have been reproduced by the generation of a suitable relativistic wave equation for the wave function as a geometric object in an appropriate geometry. This might be taken as an unfortunate consequence of the successes of Schrödinger’s wave theory. In the first paper of a series of three, Flint started with a 5-dimensional curved space with metric and an asymmetric connection:

where is the Levi-Civita connection of the 5-dimensional space, the torsion tensor, and an additional symmetric part built from torsion: 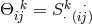[204*]. A scalar field was brought in through vector torsion: and was interpreted as a matter-wave function. The metric is demanded to be covariantly constant with regard to . In the next step, the Ricci-scalar of the 5-dimensional space is calculated. Due to (134*), it contained the 5-dimensional wave operator. Up to here, an ensuing theory for the scalar field could be imagined; so far nothing points to quantum mechanics nor to particles. By using de Broglie’s idea that the paths of massive and massless particles be given by geodesics in 5-dimensional space and O. Klein’s relation between the 5th component of momentum and electric charge, Flint was led to equate the curvature scalar to a constant containing charge, mass and Planck’s constant: Following Kaluza and Klein, was set with the Newtonian gravitational constant. The linear one-particle wave equation thus obtained contains torsion, curvature, the electromagnetic field and a classical spin tensor . It is: where is the 4-dimensional curvature scalar, , and the electromagnetic 4-potential. The particle carries charge and mass . While Flint stated that “[…] the generalized curvature, is determined by the mass and charge of the particle situated at the point where the curvature is measured” ([204], p. 420), the meaning of (136*) by no means is as trivial as claimed. A solution determines part of torsion (cf. (134*), but torsion is needed to solve (136*); we could write . Hence, (136*) is a highly complicated equation.
As a preparation for the second paper in the series mentioned [205], a link to matrix theory as developed by Schrödinger was given through replacement of the metric “by more fundamental quantities”, the 5 by 5 matrices : where the covariant derivative refers to the Levi-Civita connection of . Both formulations, with and without matrices were said “to be in harmony”. In this second paper, Dirac’s equation is given the expression with , , is replaced by . In place of (134*) now is substituted.⁶⁵ Dirac’s equation then is generalized to . The resulting wave equation of second order contains terms which could not be given a physical interpretation by Flint.
In the third paper of 1935 [206*], Flint took up the idea of “matrix length” Fock and Ivanenko had presented six years before without referring to them [215*]. now is taken to be a column and the matrix length of a vector defined to be such that with being the conjugate to . Flint seemed undecided about how to interpret . On the one hand, he said that “[…] has been interpreted as the density of matter” ([206*], p. 439), on the other he apparently had taken note of the Kopenhagen interpretation of quantum mechanics (without sharing it) when writing:

His conclusion, i.e., that quantum phenomena correspond to geometrical conceptions, and that the complete geometrical scheme includes quantum theory, gravitation, and electromagnetism could not hide that all he had achieved was to build a set of classical relativistic wave equations decorated with an . In a further paper of 1938, in the same spirit, Flint arrived at a geometrical “quantum law” built after the vanishing of the curvature scalar from which he obtained the Dirac equation in an external electrical field [207].

During the second world war, Flint refined his research without changing his basic assumption [208, 209, 210], i.e., “that the fundamental equation of the quantum theory, which is the quantum equation for an electron in a gravitational and electromagnetic field, can be developed by an appeal to simple geometric ideas.” His applications to “field theories of the electron, positron and meson” [211] and to “nuclear field theories” [212] follow the same line. No progress, either for the understanding of quantum mechanics nor for the construction of a unified field theory, can be discovered. Flint’s work was not helped by contributions of others [6, 3]. After World War II, Flint continued his ideas with a collaborator [214*]; in the meantime he had observed that Mimura also had introduced matrix length in 1935. As in a previous paper, he used the method by which Weyl had derived his first gauge theory combining gravitation and electromagnetism. Strangely enough, Weyl’s later main success, the re-direction of his idea of gauging to quantum mechanics was not mentioned by Flint although he was up to show that “equations of the form of Dirac’s equation can be regarded as gauge-equations”([214], p. 260). Under parallel transport, the matrix length of a vector is assumed to change by , where is an operator (a matrix) corresponding to the 5-vector . Flint still was deeply entrenched in classical notions when approaching the explanation of the electron’s rest mass: it should contain contributions from the electromagnetic and mesonic fields. The mathematician J. A. Schouten conjectured that “[t]he investigations of H. T. Flint are perhaps in some way connected with conformal meson theory […]” ([539*], p. 424).

That Flint was isolated from the physics mainstream may be concluded also from the fact that his papers are not cited in a standard presentation of relativistic wave-equations [84]. We dwelled on his research in order to illuminate the time lag in the absorption of new physics results among groups doing research, simultaneously. In this theme, we could have included the “tensor rear guard” (Fisher, Temple, etc.) who believed to be able to get around spinors.

4.2 Other approaches

We come back to a paper by M. Born which was referred to already in Section 3.3.2, but under a different perspective. In view of the problems of quantum field theory at the time with infinite self-energy of the electron, the zero-point energies of radiation fields adding up to infinity etc., Max Born preferred to unify quantum theory and “the principle of general invariance”, i.e., inertial fields rather than include the gravitational field. The uncertainty relations between coordinates and momenta served as a motivation for him to assume independent and unrelated metrics in configuration and in momentum space [39*]. As field equations in momentum space he postulated the Einstein field equations for a correspondingly calculated Ricci-tensor (as a function of momenta) :

The “nuclear constants” remained undetermined. Born was silent on the matter tensor. His applications of the formalism turned toward quantum electrodynamics, black body radiation and the kinetic theory of gases (of atoms). By choosing, in momentum space, the analogue to the Friedman cosmological solution with space sections of constant curvature, an upper limit for momentum ensued. The number of quantum states in volume elements of configuration space and in a volume element of momentum space turned out to be and had many consequences e.g., for Planck’s and Coulomb’s laws and for nuclear structure. The parameter b determined all deviations from previous laws: the Coulomb law for two particles became with the function and the Bessel function ; the Planck law for the energy density of black body radiation with . Born fixed such that the classical electron radius . The paper’s main result was a geometric foundation for the assumption of an upper limit for momentum – not a unification of quantum mechanics with anything else. Perhaps, Born had recycled an idea from his paper with Infeld, in which they had introduced an upper limit for the electrical field (cf. Section 5).

4.3 Wave geometry

A group of theoreticians at the Physical Institute of Hiroshima University in Japan in the second half of the 1930s intensively developed a program for a unified field theory of a new type with the intention of combining gravitation and quantum theory. Members of the group were Yositaka Mimura, Tôyomon Hosokawa, Kakutarô Morinaga, Takasi Sibata, Toranosuke Iwatsuki, Hyôitirô Takeno, and also Kyosi Sakuma, M. Urabe, K. Itimaru. The research came to a deadly halt when the first atom bomb detonated over Hiroshima, with the hypo-center of the explosion lying 1.5 km away from the Research Institute for Theoretical Physics.⁶⁶ After the second world war, some progress was made by the survivors. The theory became simplified and was summarized in two reports of the 1960s [427*, 428*].

In an introductory paper by Mimura, the new approach was termed “wave geometry” [425*]. His intention was to abandon the then accepted assumption that space-geometry underlying microscopic phenomena (like in elementary particle physics), be the same as used for macroscopic physics. Schrödinger had argued in this sense and was cited by Mimura [541]. Einstein’s original hope that space-time must not exist in the absence of matter, unfulfilled by general relativity, became revived on the level of “microscopic physics”: “[…] the microscopic space exists only when an elementary particle exists. In this sense, where there is no elementary particle, no ‘geometry’ exists” ([425*], p. 101). Also “[…] according to our new theory, geometry in microscopic space differs radically from that of macroscopic […]” ([425], p. 106).⁶⁷ “wave geometry” must not be considered as one specific theory but rather as the attempt for a theory expressing the claimed equivalence of geometry and physics.

The physical system, “the space-time-matter” manifold, was to be seen as a (quantum mechanical) state , a 4-component (Dirac) spinor; “distance” in microscopic space became defined as an eigenvalue of a linear distance operator. In order to find this operator, by following Dirac, a principle of linearization was applied:

with where is an arbitrary tetrad (with the tetrad index ), and denoting the Dirac matrices. If is demanded, i.e., the eigenvalues of the distance operator are . If Riemannian covariant differentiation is used, then Here, denotes the spin connection. As the fundamental equation of the theory was written down where is an as yet undetermined 4-vector with matrix entries. It was expected that (144*) describe the gravitational, electromagnetic and the matter field “in unified form not discriminating macroscopic and microscopic phenomena” ([427*], p. 11). In 1929, (140*) had also been suggested by Fock and Ivanenko [215], a paper mentioned briefly in Section 7.2 of Part I. As we have seen, at around the same year 1935, H. T. Flint had set up a similar unified theory as Mimura [206]. The theory of Mimura and Takeno was to be applied to the universe, to local irregularities (galaxies) in the universe and to the atom. Only the Einstein cosmos and de Sitter space-time were allowed as cosmological metrics. For the atom, a solution in a space-time with metric was obtained and a wave function “which can be identified with the Dirac level of the hydrogen atom if the arbitrary functions and constants in the equation are chosen suitably” ([427], p. 66). With a particular choice of , (cf. [428*], Eq. 4.15 on p. 4) the fundamental equation for was then determined to be the matrix equation: with . and are arbitrary vectors. In [428*], a second fundamental equation was added: with a scalar . For complete integrability of (145*), the Riemannian curvature tensor must vanish. Equation (145*) reduces to with the solution . This being too restrictive, (145*) was weakened to for either or with the integrability conditions , respectively. T. Sibata gave a solution of this equation expressing self-duality for weak fields [576]. He also set out to show that Born–Infeld theory follows from his approach to wave geometry in the case of vacuum electrodynamics [577]. In this paper, the condition of complete integrability for his version of (144*) read as .

In 1938, T. Hosokawa even had extended wave geometry to Finsler geometry and applied to Milne’s cosmological principle [287*].

With its results obtained until 1945, wave geometry could not compete with quantum field theory. After the war, the vague hope was expressed that in a “supermicroscopic” space-time, elementary particle theory could be developed and that “the problem of internal space’ of elementary particles may be interwoven with some ‘hidden’ relations to the structure of space-time.”([428*], p. 41.) Clearly, the algebra of -matrices which is all what is behind the distance operator, was an insufficient substitute for the algebra of non-commuting observables in quantum field theory.