1 Introduction
The dream of unifying all fundamental interactions in a single theory by one common representation still captures the mind of many a theoretical physicist. In the following, I will focus on the development of classical unified field theory (UFT) in the period from the mid-1930s to the mid-1960s. One of the intentions then was to join the gravitational to the electromagnetic field, and, hopefully, to other fields (mesonic, …) in “a single hyperfield, whose basis would be equivalent to that of the geometrical structure for the universe” ([376], p. 3). Einstein referred to his corresponding theories alternatively as the “generalized theory of gravitation”, “(relativistic) theory of the non-symmetric (or asymmetric) field”, and of “the theory of the total field”. Schrödinger spoke of “unitary field theory”; this name was taken up later by Bergmann [24] or Takasu [598*]. In Mme. Tonnelat’s group, the name “théorie du champ unifié d’Einstein” (or d’Einstein–Schrödinger), or just “théorie unitaire (du champ)(d’Einstein)” was in use; Hlavatý called it “(Einstein) Unified (Field) Theory of Relativity”. In other papers we read of “Einstein’s Generalized Theory of Gravitation”, “Einstein’s equations of unified field”, “theory of the non-symmetric field”, “einheitliche Feldtheorie” etc. However, we should not forget that other types of unitary field theory were investigated during the period studied, among them Kaluza–Klein theory and its generalizations. In France, one of these ran under the name of “Jordan–Thiry” theory, cf. Sections 3.1.2 and 11.1. Most important centers for research on unified field theory in the 1930s until the early 1950s were those
around Albert Einstein in Princeton and Erwin Schrödinger in Dublin. Paris became a focus of UFT in the
late 1940s up to the late 1960s, with a large group of students around both Mme. M.-A. Tonnelat in
theoretical physics, and the mathematician A. Lichnerowicz. In comparison with the work of Einstein and
Schrödinger, the contributions to UFT of the Paris groups have been neglected up to now by historians of
physics although they helped to clarify consequences of the theory. These groups had a share both in the
derivation of exact mathematical results and in contributing arguments for the eventual demise of
UFT. The mathematician V. Hlavatý from Indiana University, Bloomington (USA), with
one or two students, enriched the mathematically-oriented part of the UFT-community with
his systematical studies in the 1950s. We will encounter many further researchers worldwide,
especially sizeable groups in Italy, and in countries like Canada, England, India, and Japan.
The time period is chosen such that Einstein’s move from Berlin to Princeton approximately
defines its beginning while its end falls into the 1960s which saw a revival of interest in general
relativity theory [192], and the dying off of some still existing interest into classical unified field
theory. Up to the 1940s, some hope was justified that the gravitational interaction might play
an important role in the unification of the fundamental fields. With the growth of quantum
field theory and developments in elementary particle physics, gravity became crowded out,
however.
At the time, the mainstream in theoretical physics had shifted to quantum mechanics and its applications in many parts of physics and physical chemistry. Quantum field theory had been invented as a relevant tool for describing the quantum aspects of atoms, molecules and their interactions with P. Jordan, M. Born and W. Heisenberg having made first steps in 1926. Dirac had put forward his “second” quantization in 1927 which was then interpreted and generalized as field quantization by Jordan, Heisenberg, Klein, Pauli, and Wigner in 1927/28. Expert histories of quantum electrodynamics and its beginning have been presented1 by S. Schweber [562], O. Darrigol [109], and A. Pais [470]. Around the time when Einstein left Berlin, Heisenberg and others set up theories of the strong nuclear force. Fermi had introduced a theory of weak interactions in connection with beta-decay. Since 1932/33, besides electron, photon, and proton, three new particles, namely the neutron, positron and neutrino had come into play with the last two already having been found, empirically. Anyone doubting the existence of the neutron, had to give in after nuclear fission had been discovered and nuclear reactors been built. At the 1933 Solvay conference, L. de Broglie had proposed a neutrino theory of light, i.e., with the photon as a composite particle made up by two neutrinos [111, 112], and others like P. Jordan or G. Wentzel had followed suit [314, 315, 687]. For a while, this became a much debated subject in theoretical physics. Another great topic, experimentally, was the complicated physics of “cosmic rays” containing at least another new particle with a mass about 200 times that of the electron. It was called alternatively “heavy electron”, “mesot(r)on”, and “meson” and became mixed up with the particle mediating the nuclear force the name of which was “U-quantum”, or “Yukon” after Yukawa’s suggestion in 1934/35 concerning nuclear interactions. For the history cf. [63]. When the dust had settled around 1947, the “mesotron” became the muon and the pions were considered to be the carriers of the nuclear force (strong interaction). Since 1937, the muon had been identified in cosmic rays [455, 593]. The charged pion which decays into a muon and a (anti-)neutrino via the weak interaction was detected in 1947, the uncharged one in 1950. In the 1940s, quantum electrodynamics was given a new kick by Feynman, Schwinger and Tomonaga. Up to the mid fifties, nuclear theory had evolved, the strong and weak nuclear forces were accepted with the neutrino observed only in 1957, after Einstein’s death. Thus, the situation had greatly changed during the two decades since Einstein had started to get involved in unified field theory: in the 1920s only two fundamental interactions had been known, both long-range: the electromagnetic and the gravitational. Before 1926, neither non-relativistic quantum theory, nor relativistic quantum electrodynamics had been developed. In 1928, with Dirac’s equation, “spin” had appeared as a new property of elementary particles. After a brief theoretical venture into spinors and the Dirac equation (cf. Section 7.3 of Part I and Section 4.1), against all of the evidence concerning new particles with half-integer spin and new fundamental interactions obtained in the meantime, Einstein continued to develop the idea of unifying only the electromagnetic and gravitational fields via pure geometry, cf. Section 7 below. His path was followed in much of the research done in classical UFT. Occasionally, as in Schrödinger’s and Tonnelat’s work, meson fields, treated as classical fields, were also included in the interpretation of geometric objects within the theory. The state of affairs was reflected, in 1950, in a note in the Scientific American describing Einstein’s motivation for UFT as:
“to relate the physical phenomena in the submicroscopic world of the atom to those in the macroscopic world of universal space-time, to find a common principle explaining both electromagnetic forces and gravitational force […]. In this inquiry Einstein has pursued a lonely course; most physicists have taken the apparently more promising road of quantum theory.” ([564*], p. 26)
In fact, the majority of the theoretical physicists working in field theory considered UFT of the
Einstein–Schrödinger type as inadequate. Due to Einstein’s earlier achievements, his fame and,
possibly, due to his, Schrödinger’s and de Broglie’s reserve toward the statistical interpretation
of quantum mechanics, classical or semi-classical approaches to field theory were favoured in
their scientific research environments in theoretical physics. Convinced by the stature of these
men, a rather small number of theoretical physicists devoted their scientific careers to classical
unified field theory. Others wrote their PhD theses in the field and then quickly left it. A few
mathematicians became attracted by the geometrical structures underlying the field (cf. [677],
p. 30).
In their demands on UFT, Einstein and Schrödinger differed: while the first one never gave up his hope to find a substitute, or at least a needed foundation for quantum theory in his classical unified field theory, Schrödinger saw his theory as a strictly classical groundwork for an eventual alternative to quantum field theory or, as he expressed it himself, as “ ‘the classical analogue’ of the true laws of Nature” ([551*], p. 50).2 Einstein in particular followed his way towards UFT unwaveringly in spite of failing success. Shortly before his death, he even reinterpreted his general relativity, the central concept of which had been the gravitational and inertial potentials encased in the (pseudo-)Riemannian metric tensor, through the lens of unified field theory:
“[…] the essential achievement of general relativity, namely to overcome ‘rigid’ space (i.e.,
the inertial frame), is only indirectly connected with the introduction of a Riemannian
metric. The direct relevant conceptual element is the ‘displacement field’ (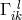 ), which
expresses the infinitesimal displacement of vectors. It is this which replaces the parallelism
of spatially arbitrarily separated vectors fixed by the inertial frame (i.e., the equality
of corresponding components) by an infinitesimal operation. This makes it possible to
construct tensors by differentiation and hence to dispense with the introduction of ‘rigid’
space (the inertial frame). In the face of this, it seems to be of secondary importance
in some sense that some particular
), which
expresses the infinitesimal displacement of vectors. It is this which replaces the parallelism
of spatially arbitrarily separated vectors fixed by the inertial frame (i.e., the equality
of corresponding components) by an infinitesimal operation. This makes it possible to
construct tensors by differentiation and hence to dispense with the introduction of ‘rigid’
space (the inertial frame). In the face of this, it seems to be of secondary importance
in some sense that some particular 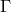 -field can be deduced from a Riemannian metric
[…].”3
-field can be deduced from a Riemannian metric
[…].”3 (A. Einstein, 4 April 1955, letter to M. Pantaleo, in ([473*], pp. XV–XVI); English translation
taken from Hehl and Obuchov 2007 [244].)
(A. Einstein, 4 April 1955, letter to M. Pantaleo, in ([473*], pp. XV–XVI); English translation
taken from Hehl and Obuchov 2007 [244].)
To me, this is not a prophetic remark pointing to Abelian and non-Abelian gauge theories which turned out to play such a prominent role in theoretical physics, a little later.4 Einstein’s gaze rather seems to have been directed backward to Levi-Civita, Weyl’s paper of 1918 [688], and to Eddington.5 The Institute for Advanced Study must have presented a somewhat peculiar scenery at the end of the 1940s and early 50s: among the senior faculty in the physics section as were Oppenheimer, Placzek and Pais, Einstein remained isolated. That a “postdoc” like Freeman Dyson had succeeded in understanding and further developing the different approaches to quantum electrodynamics by Schwinger and Feynman put forward in 1948, seemingly left no mark on Einstein. Instead, he could win the interest and help of another Princeton postdoc at the time, Bruria Kaufman, for his continued work in UFT [587]. We may interpret a remark of Pauli as justifying Einstein’s course:
“The quantization of fields turns out more and more to be a problem with thorns and
horns, and by and by I get used to think that I will not live to see substantial progress for
all these problems.” ([493*], p. 519)6
In fact, for elementary particle theory, the 1950s and 1960s could be seen as “a time of frustration and
confusion” ([686], p. 99). For weak interactions (four-fermion theory) renormalization did not
work; for strong interactions no calculations at all were possible. W. Pauli was very skeptical
toward the renormalization schemes developed: “[…] from my point of view, renormalization
is a not yet understood palliative.” (Letter to Heisenberg 29 September 1953 [491*], p. 268.)
About a month after Einstein’s death, the mathematician A. Lichnerowicz had the following to say concerning his unified field theory:
“Einstein just has disappeared leaving us, in addition to many completed works, an
enigmatic theory. The scientists look at it – like he himself did – with a mixture of distrust
and hope, a theory which carries the imprint of a fundamental ambition of its creator.”
(cf. Lichnerowicz, preface of [632*], p. VII.)7
In Bern, Switzerland, three months after Einstein’s death, a “Jubilee Conference” took place commemorating fifty years of relativity since the publication of his famous 1905 paper on the electrodynamics of moving bodies. Unified field theory formed one of its topics, with 34 contributions by 32 scientists. In 1955, commemorative conferences were also held in other places as well which included brief reviews of UFT (e.g., by B. Finzi in Bari [203*] and in Torino [203*]). Two years later, among the 21 talks of the Chapel Hill Conference on “the role of gravitation in physics” published [119], only a single one dealt with the “Generalized Theory of Gravitation” [344]. Again five years later, after a conference on “Relativistic Theories of Gravitation”, the astronomer George C. McVittie (1904 – 1988) could report to the Office of Naval Research which had payed for his attendance: “With the death of Einstein, the search for a unified theory of gravitation and electromagnetism has apparently faded into the background.” (Quoted in [523], p. 211.) This certainly corresponded to the majority vote. At later conferences, regularly one contribution or two at most were devoted to UFT [302*, 382*]. From the mid-1960s onward or, more precisely, after the Festschrift for V. Hlavatý of 1966 [282], even this trickle of accepted contributions to UFT for meetings ran dry. “Alternative gravitational theories” became a more respectable, but still a minority theme. Not unexpectedly, some went on with their research on UFT in the spirit of Einstein, and some are carrying on until today. In particular, in the 1970s and 80s, interest in UFT shifted to India, Japan, and Australia; there, in particular, the search for and investigation of exact solutions of the field equations of the Einstein–Schrödinger unified field theory became fashionable. Nevertheless, Hlavatý’s statement of 1958, although quite overdone as far as mathematics is concerned, continues to be acceptable:
“In the literature there are many approaches to the problem of the unified field theory. Some of them strongly influenced the development of geometry, although none has received general recognition as a physical theory.” ([269*], preface, p. X.)
The work done in the major “groups” lead by Einstein, Schrödinger, Lichnerowicz, Tonnelat, and Hlavatý was published, at least partially, in monographs (Einstein: [150*], Appendix II; [156*], Appendix II); (Schrödinger: [557*], Chapter XII); (Lichnerowicz: [371*]); (Hlavatý: [269*]), and, particularly, (Tonnelat: [632*, 641*, 642*]). To my knowledge, the only textbook including the Einstein–Schrödinger non-symmetric theory has been written in the late 1960s by D. K. Sen [572*]. The last monograph on the subject seems to have been published in 1982 by A. H. Klotz [334]. There exist a number of helpful review articles covering various stages of UFT like Bertotti [26], Bergia [19*], Borzeszkowsi & Treder [679], Cap [71], Hittmair [256*], Kilmister and Stephenson [330, 331*], Narlikar [453], Pinl [497], Rao [504*], Sauer [528, 529], and Tonnelat ([645*], Chapter 11), but no attempt at giving an overall picture beyond Goenner [228] seems to have surfaced. Vizgin’s book ends with Einstein’s research in the 1930s [678]. In 1957, V. Bargmann has given a clear four-page résumé of both the Einstein–Schrödinger and the Kaluza–Klein approaches to unified field theory [12*].8 In van Dongen’s recent book, the epistemological and methodological positions of Einstein during his work on unified field theory are discussed [667*].
The present review intends to provide a feeling for what went on in research concerning UFT at the time, worldwide. Its main themes are the conceptual and methodical development of the field, the interaction among the scientists working in it, and their opinions and interpretations. The review also includes a few sections on the fringes of the general approach. A weighty problem has been to embed the numerous technical details in a narrative readable to those historians of science lacking the mathematical tools which are required in many sections. In order to ease reading of chapters, separately, a minor number of repetitions was deemed helpful. Some sociological and philosophical questions coming up in connection with this review will be touched in Sections 18 and 19. These two chapters can be read also by those without any knowledge of the mathematical and physical background. Up to now, philosophers of science apparently have not written much on Einstein’s unified field theory, with the exception of remarks following from a non-technical comparison of the field with general relativity. Speculation about the motivation of the central figures are omitted here if they cannot be extracted from some source.
The main groups involved in research on classical unified field theory will be presented here more or
less in chronological order. The longest account is given of Einstein–Schrödinger theory. In
the presentation of researchers we also follow geographical and language aspects due to
publications in France being mostly in French, in Italy mostly in Italian, in Japan and India in
English.9
We cannot embed the history of unified field theory into the external (political) history of the period
considered; progress in UFT was both hindered by the second world war, Nazi- and communist regimes, and
helped, after 1945, by an increasing cooperation among countries and the beginning globalization of
communications.10
Part II of the “History of Unified Field Theory” is written such that it can be read independently from Part I. Some links to the earlier part [229] in Living Reviews in Relativity are provided.