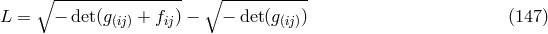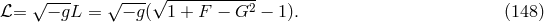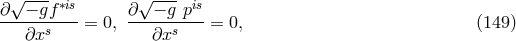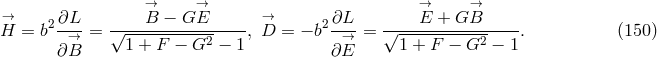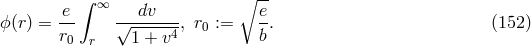5 Born–Infeld Theory
In 1934, M. Born and L. Infeld published a paper on “The Foundations of the New Field Theory” [42*]. Its somewhat vague title hid a non-linear theory of the electromagnetic field using a non-symmetric metric but denying a relationship with “ ‘unitary‘ field due to Einstein, Weyl, Eddington, and others […]”. In fact, the original idea for the new theory originated in July 1933 while Born was still a member of the University of Göttingen but already on the move from Germany for vacations in South Tyrol to only return after World War II. Born’s next publication, submitted in August 1933 without institutional address, dealt with the quantization of the electromagnetic field; in it the new Lagrangian was also shown [37*]. In view of the problems with divergent terms in quantum (field) electrodynamics at the time, he set out to modify Maxwell’s equations in such a way that an electron with finite radius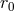 could be described; its electric potential remained finite for
could be described; its electric potential remained finite for 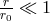 [36]. The
Lagrangian for the new electrodynamics was
[36]. The
Lagrangian for the new electrodynamics was 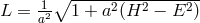 with the constant a of
dimension
with the constant a of
dimension 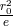 , where
, where  is the elementary electric charge and
is the elementary electric charge and 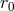 the electron radius. In the
limit
the electron radius. In the
limit 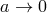 the Lagrangian of Maxwell’s theory reappeared:
the Lagrangian of Maxwell’s theory reappeared: 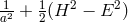 . In the
paper with Infeld, the Lagrangian is generalized in order to include the gravitational field:
where
. In the
paper with Infeld, the Lagrangian is generalized in order to include the gravitational field:
where 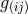 is the (Riemannian) metric and
is the (Riemannian) metric and ![fij = f[ij]](article723x.gif) the electromagnetic field tensor;
the electromagnetic field tensor; 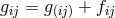 ,
formally is an asymmetric metric. The Lagrangian (147*) can be expressed by the two invariants of
Maxwell’s theory
,
formally is an asymmetric metric. The Lagrangian (147*) can be expressed by the two invariants of
Maxwell’s theory 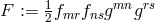 and
and 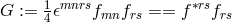 as
The new field equations become:
with the definition
as
The new field equations become:
with the definition 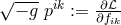 . Insertion of
. Insertion of 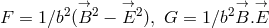 led to Maxwell’s
equations plus the relations between fields and inductions:
“The quotient of the field strength expressed in the conventional units divided by the field strength in the
natural units” was denoted by
led to Maxwell’s
equations plus the relations between fields and inductions:
“The quotient of the field strength expressed in the conventional units divided by the field strength in the
natural units” was denoted by 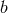 and named the “absolute field”. As was well known, many asymmetric
energy-momentum tensors for the electromagnetic field could be formulated. Years later, St. Mavridès
took up this problem and derived identities for the symmetric Minkowski tensor, the fields and
inductions, independent of whether the relations between fields and inductions were linear or
more general [410]. Xinh Nguyen Xua then showed that with the relations (150*), all the various
energy-momentum tensors can be derived from one such symmetric tensor [711]. Born & Infeld chose
The static solution of the new equations for the potential of a point charge was determined to be
It turned out that, from
and named the “absolute field”. As was well known, many asymmetric
energy-momentum tensors for the electromagnetic field could be formulated. Years later, St. Mavridès
took up this problem and derived identities for the symmetric Minkowski tensor, the fields and
inductions, independent of whether the relations between fields and inductions were linear or
more general [410]. Xinh Nguyen Xua then showed that with the relations (150*), all the various
energy-momentum tensors can be derived from one such symmetric tensor [711]. Born & Infeld chose
The static solution of the new equations for the potential of a point charge was determined to be
It turned out that, from 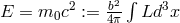 ,
, 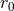 could be calculated numerically via
could be calculated numerically via
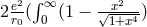 to take the value
to take the value 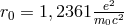 and thus
and thus 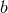 could also be determined. According
to Born and Infeld: “The new field theory can be considered as a revival of the old idea of the
electromagnetic origin of mass” Also, the existence of an absolute field as a “natural unit for
all field components and the upper limit for a purely electric field” ([42*], p. 451) had been
assumed.
could also be determined. According
to Born and Infeld: “The new field theory can be considered as a revival of the old idea of the
electromagnetic origin of mass” Also, the existence of an absolute field as a “natural unit for
all field components and the upper limit for a purely electric field” ([42*], p. 451) had been
assumed.
Unsurprisingly, Pauli was unhappy with the paper by Born and Infeld as far as its inclusion of the
gravitational field via 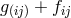 was concerned. Instead, in his letter of 21 December 1933 to Max Born ([488*],
p. 241), he suggested to take as a Lagrangian density
was concerned. Instead, in his letter of 21 December 1933 to Max Born ([488*],
p. 241), he suggested to take as a Lagrangian density 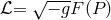 with Kaluza’s curvature scalar in 5
dimensions
with Kaluza’s curvature scalar in 5
dimensions 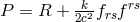 . “In particular, it is possible to set
. “In particular, it is possible to set 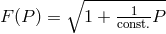 , and therefore
your electrodynamics is compatible with the projective view on the electromagnetic and gravitational
field.”68
, and therefore
your electrodynamics is compatible with the projective view on the electromagnetic and gravitational
field.”68 But for Born, electrodynamics was in the focus. Three months after Pauli’s criticism, he wrote to Einstein
in connection with his paper with Infeld:
But for Born, electrodynamics was in the focus. Three months after Pauli’s criticism, he wrote to Einstein
in connection with his paper with Infeld:
“Possibly, you will not agree, because I do not include gravitation. This is a rather
basic point, where I have a different view as you in your papers on unitary field theory.
Hopefully, I soon will be able to finalize my idea on gravitation” ([168*], p. 167).69
Around the same time as Pauli, B. Hoffmann who had left Princeton for the University of
Rochester, had had the same idea. It was couched in the language of projective theory
on which he had worked with O. Veblen (cf. Section 6.3.2 of Part I) and on his own
[275*].70
He suggested the Lagrangian 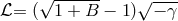 where
where 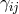 is the 5-dimensional projective metric
and
is the 5-dimensional projective metric
and 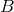 the projective curvature scalar. Due to
the projective curvature scalar. Due to 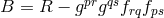 , his Lagrangian corresponds to
Kaluza’s. Born & Infeld had remarked that in order to include gravitation in their theory, only Einstein’s
Lagrangian must be added to (148*). Hoffmann now tried to obtain a static spherically symmetric solution
for both theories with a non-vanishing electromagnetic field. In the augmented Born–Infeld
Lagrangian, the Minkowski metric could be used as a special case. According to Hoffmann this was no
longer possible for his Lagrangian because “the electromagnetic field exerts a gravitational
influence” ([275], p. 364). As he could not find a solution to his complicated field equations, the
“degree of modification of the electrostatic potential by its own gravitational field” could not be
determined.
, his Lagrangian corresponds to
Kaluza’s. Born & Infeld had remarked that in order to include gravitation in their theory, only Einstein’s
Lagrangian must be added to (148*). Hoffmann now tried to obtain a static spherically symmetric solution
for both theories with a non-vanishing electromagnetic field. In the augmented Born–Infeld
Lagrangian, the Minkowski metric could be used as a special case. According to Hoffmann this was no
longer possible for his Lagrangian because “the electromagnetic field exerts a gravitational
influence” ([275], p. 364). As he could not find a solution to his complicated field equations, the
“degree of modification of the electrostatic potential by its own gravitational field” could not be
determined.
In connection with the work of Euler and Kockel on the scattering of light by light under his guidance,
W. Heisenberg wrote Pauli on 4 November 1934: “The terms to be added to the Lagrangian look like in the
theory of Born and Infeld, but they are twenty times larger than those of Born and Infeld” ([488*],
p. 358).71 But Pauli had not changed his opinion; in connection with the scattering of light by light, he answered
Heisenberg curtly: “I do not care about Born’s theory” ([488], p. 372). Ten years later, in his
letter to Einstein of 10 October 1944 Born assessed his theory with some reservation ([168*],
p. 212):
But Pauli had not changed his opinion; in connection with the scattering of light by light, he answered
Heisenberg curtly: “I do not care about Born’s theory” ([488], p. 372). Ten years later, in his
letter to Einstein of 10 October 1944 Born assessed his theory with some reservation ([168*],
p. 212):
“[…] I always had a lot of understanding for your good Jewish physics, and much amusement
with it; however, I myself have produced it only once: the non-linear electrodynamics, and
this is no particular success […].”72
Nevertheless, it had some influence on UFT; cf. Sections 6.1.3, 9.7, and 10.3.4.
Born and Infeld unsuccessfully tried to quantize their non-linear theory of the electromagnetic field by
using the commutation rules of Heisenberg and Pauli for the field strenghts [43, 44]. They noticed that the
theory could be presented differently according to whether the pairs 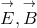 , or
, or 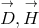 ;
; 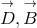 ;
; 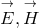 were chosen as independent variables. The authors took
were chosen as independent variables. The authors took 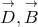 in order to avoid “formal difficulties”.
However, a perturbative approach by canonical quantization of either the field or the vector potential could
not succeed because the interaction term in the Hamiltonian included higher powers of derivative
terms.73
in order to avoid “formal difficulties”.
However, a perturbative approach by canonical quantization of either the field or the vector potential could
not succeed because the interaction term in the Hamiltonian included higher powers of derivative
terms.73
One who became attracted by the Born–Infeld theory was E. Schrödinger. He had come “across a
further representation, which is so entirely different from all the aforementioned, and presents such curious
analytical aspects, that I desired to have it communicated” ([542], p. 465). He used a pair 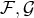 of
complex combinations of the 3-vector fields
of
complex combinations of the 3-vector fields 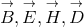 such that
such that 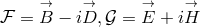 .
The Lagrangian
.
The Lagrangian 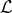 was to be determined such that its partial derivatives with respect to
was to be determined such that its partial derivatives with respect to
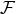 and
and 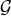 coincided with the complex conjugates:
coincided with the complex conjugates: 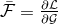 and
and 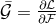 . The result is
. The result is
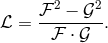
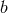 was set equal to one. Schrödinger showed that his formulation was “entirely equivalent
to Born’s theory” and did not provide any further physical insight. Thus, Schrödinger’s paper gave a witty
formal comment on the Born–Infeld theory. Ironically, it had been financed by Imperial Chemical
Industries, Limited.
was set equal to one. Schrödinger showed that his formulation was “entirely equivalent
to Born’s theory” and did not provide any further physical insight. Thus, Schrödinger’s paper gave a witty
formal comment on the Born–Infeld theory. Ironically, it had been financed by Imperial Chemical
Industries, Limited.
S. Kichenassamy74
studied the subcase of an electromagnetic null field with matter tensor: 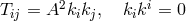 and
showed that in this case the Born–Infeld theory leads to the same results as Maxwell’s electrodynamics
[328, 340].
and
showed that in this case the Born–Infeld theory leads to the same results as Maxwell’s electrodynamics
[328, 340].