19 On the Conceptual and Methodic Structure of Unified Field Theory
From his varied attempts at a unified field theory during the decades covered both in Part I and Part II of this review, it may be concluded that in this field of research Einstein never had or followed a program, in the strict sense, over a longer period of time. He seems to have been resistant to external influences as were, e.g., the fashionable attempts at an inclusion of the meson into all sorts of unitary field theory. Whether the last decade of his research pursuing structural investigations within mixed geometry and directed toward the establishment of field equations, as firmly grounded as his field equations of general relativity, is characterized by “enlightened perseverance” or “biased stubbornness” lies in the eye of the beholder. We shall now try to look from a more general point of view at the detailed and technical discussions given above.
19.1 General issues
Advantages of a theory unifying other theories are: (1) the conceptual structure of the unified theory will in general be richer, (2) its empirical content more inclusive, and (3) the limits of application of the sub-theories covered easier to determine ([221], p. 273, 276). On the first point UFT performs too well: The various forms of Einstein–Schrödinger unified field theory all provide us with too many mathematical objects as to allow a convincing selection of an unambiguous geometrical framework for a physical theory. To quote M.-A. Tonnelat:
“The multiplicity of structural elements brought into the game, the arbitrariness reigning
over their interpretation, bring an unease into the theory which one cannot lightly make
vanish in total.”([641*], p. 299.)318
In addition, particularly within mixed (or even metric-affine) geometry, the dynamics is highly arbitrary,
i.e., possible field equations abound. Usually, the Lagrangian is built after the Lagrangian of general
relativity, possibly because this theory was required to emerge from UFT in some limiting process. But
L. A. Santalò has shown that the “weak” field equations can be reached from a Lagrange function
linear in curvature and quadratic in torsion containing 5 free parameters ([524], Theorem 2,
p. 350).319
There exists a 3-parameter Lagrangian which is transposition invariant and also leads to the “weak” system
(p. 352). The same author has also proven that there are Lagrangians of the same class which are not
invariant under 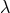 -transformations (cf. Section 2.2.3) but still lead to the “weak” field equations (p. 351,
Theorem 3). Thus, in spite of all symmetry- and plausibility arguments put forward, none of the field
equations used by Einstein and Schrödinger acquired an equivalent position of uniqueness like the field
equations of general relativity.
-transformations (cf. Section 2.2.3) but still lead to the “weak” field equations (p. 351,
Theorem 3). Thus, in spite of all symmetry- and plausibility arguments put forward, none of the field
equations used by Einstein and Schrödinger acquired an equivalent position of uniqueness like the field
equations of general relativity.
As to the 2nd and 3rd points, even if UFT had succeeded as a theory with a well-put particle concept, by the 1940s the newly discovered particles (neutron, mesons, neutrino) would have required another approach taking into account the quantum nature of these particles. Field quantization had been successfully developed for this purpose. Occasionally, the argument has been made that a unification of the two long-range fundamental forces within classical theory would have been enough to be asked for in “pre-quantum physics” ([234], p. 255). However, the end of pre-quantum physics must be set not later than 1925/26; in particular, the development of quantum electrodynamics had started already at the end of the 1920s; it is now part of the partial unification achieved by the Glashow–Salam–Weinberg model (1967). Certainly, quantum field theory suffered from severe problem with infinities to be removed before the observables of the theory could provide numbers to be compared with measurements. At last, renormalization procedures did the job so well that an effect like the Lamb-shift could be calculated, with the inclusion of self-energy contributions, up to highest precision.320
Unlike this, the UFTs of the 1920s to the 1940s did not get to the stage where empirical tests could have been made. Actually, in later developments novel gravito-electromagnetic effects were derived from UFT; cf. Sections 6.1.2, 15.2. Unfortunately, they never led to observed results. Often, it is argued unconvincingly that this is due to the weakness of the gravitational field; for either a strong electrical or a strong gravitational field (neutron stars), measurable effects of the interaction of these fields could have been expected. In a way, UFT of the Einstein–Schrödinger type was as removed from an empirical basis then as quantum cosmology or string theory are at present. Pauli had been aware of this already in the 30s ([489*], p. 789):
“It is odd how Einstein carries on physics nowadays. In effect, it is the method of a pure
mathematician decreeing all from his desk who completely has lost contact with what
physicists really do.”321
Ironically, when H. Weyl had suggested his generalization of Riemannian geometry by a purely mathematical argument, and then had used it to build a theory unifying gravitation and electromagnetism (cf. Section 4.1 of Part I), Einstein had refuted him for not having thought of the empirical consequences. Now, he followed the same course: He started from a mathematical structure and then aimed at turning it into a physical theory. There is a difference, though, because for his own theory Einstein was not able to derive testable consequences:
“The unified field theory now is self-contained. But its mathematical application is so
difficult that I have not been capable to test it in some way in spite of all the efforts
invested.” (Letter to M. Solovine 12 February 1951, in [160], p. 106.)322
The speculative character of UFT was rendered yet more unattractive by its unsolved problems: how to describe matter, in particular the motion of charged particles. Doubts came up very early whether the Lorentz force could be extracted from the theory in the lowest steps of a non-trivial approximation. Instead of winning new results, many authors were content when they were able to reproduce effects already known from general relativity and Maxwell’s theory; cf. Section 15.3. The missing empirical support was critically seen even within the community of workers in unified field theory:
“Unified theories do suggest to base the electromagnetic and gravitational fields on one
and the same hyper-field – with the physical phenomena being explained by a geometrical
structure imposed on space-time, independently from any phenomenological hypothesis.
The ambition of such an explication in the spirit of Cartesian philosophy is recognized
which, far from following the observational and experimental results step by step, pretends
to anticipate them. The theory incorporates its actual provisions into a vast synthesis
and furnishes them with a whole program of a posteriori verifications.” ([94], p. 331)
323
Due to his epistemological and methodical position, Einstein could not have cared less. With no empirical data around, he fitted the envisaged UFT to the various mathematical structural possibilities. As has been shown in great detail, originally, when struggling with a relativistic theory of gravitation, he had applied two methods: “induction from the empirical data” and “mathematical deduction” ([309], p. 500–501). In his later work, he confined himself to the second one by claiming that only mathematical simplicity and naturalness could lead to a fundamental theory reflecting unity. Intuition is played down by him in favour of quasi-axiomatic principles. This shift in Einstein’s epistemology and methodology has been described in detail by J. D. Norton [458], D. Howard [290], and J. van Dongen [667]. However, we should not forget that both concepts, simplicity and naturalness, lack unambiguous mathematical or philosophical definitions.
In this context, Einstein’s distinction between “constructive theories” and “theories of principle” may also be considered. The first ones are constructive, they “[…] attempt to build up a picture of the more complex phenomena out of the materials of a relatively simple formal scheme from which they start out […]”. The second important class called principle-theories “employ the analytic, not the synthetic, method. The elements which form their basis and starting-point are not hypothetically constructed but empirically discovered ones, general characteristics of natural processes, principles that give rise to mathematically formulated criteria which the separate processes or the theoretical representations of them have to satisfy.” ([157], p. 228) According to Einstein, the theory of relativity belongs to the second class with its “logical perfection and security of the foundations”. His unified field theory fits better to the description of a constructive theory.
The more delicate question why the unification of the fundamental forces must be sought by a geometrization of the fields, was rarely asked. In Weyl’s approach, a pre-established harmony between mathematics and physics had been put forward as an argument. Y. Mimura and T. Hosokawa saw the “mission of physics” in looking for answers to the questions: “What is space-time in the world wherein physical phenomena occur?” and “By what laws are those physical phenomena regulated?” Their idea was that the properties of space-time are represented by physical laws themselves. “Thus theoretical physics becomes geometry. And that is why physical laws must be geometrized” ([426], p. 102). This circular remark of 1939 is less than convincing. Other paths could have been followed (and later were), e.g., one along a unifying (symmetry) group.324 A renowned scientist like P. A. M. Dirac shied away altogether from such a big sweep as unification is. He favoured an approximative approach to an eventually all encompassing theory: “One should not try to accomplish too much in one stage. One should separate the difficulties in physics one from another as far as possible, and then dispose of them one by one” ([125], quoted from [338], p. 373). On aesthetical grounds, Dirac came closer to Einstein:
“It seems to be one of the fundamental features of nature that fundamental physical laws are described in terms of a mathematical theory of great beauty and power, needing quite a high standard of mathematics for one to understand it. You may wonder: Why is nature constructed along these lines? One can only answer that our present knowledge seems to show that nature is so constructed. We simply have to accept it.” [124].
When Einstein geometrized gravitation, he had a good argument in the equality of inertial and gravitational mass. For electrodynamics and UFT, no such argument has been presented. In the 1950s, “charge-independence” as a property of strong interactions between baryons and mesons was discussed but not used for geometrization.325
19.1.1 What kind of unification?
According to Bargmann, the aim of UFT was: “(1) to deduce, at least in principle, all physical interactions from one law, (2) to modify the field equations in such a way that they would admit solutions corresponding to stable charged particles” ([12], p. 169). This general description of Einstein’s eventual course for describing fundamental aspects of physical reality (nature) by one single theory can be complemented by further, more specific, details.
In Sections 8.1 and 10.3.4 we have mentioned Pauli’s criticism with regard to the use of
![g = h + k ij (ij) [ij]](article3084x.gif) in Einstein’s and some of Schrödinger’s unified field theories. As Mme. Tonnelat noted,
this meant that the theory is unified only in “a weak sense” because the gravitational and electromagnetic
fields are represented by different geometrical objects. Apart from the demand that the fundamental field
quantities (metric, …) must be irreducible with regard to the diffeomorphism group, Einstein had claimed
symmetry with regard to
in Einstein’s and some of Schrödinger’s unified field theories. As Mme. Tonnelat noted,
this meant that the theory is unified only in “a weak sense” because the gravitational and electromagnetic
fields are represented by different geometrical objects. Apart from the demand that the fundamental field
quantities (metric, …) must be irreducible with regard to the diffeomorphism group, Einstein had claimed
symmetry with regard to 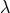 -transformations, because these would mix the symmetric and
skew-symmetric parts of the connection and thus counter criticism of the type Pauli had phrased. A
further necessary condition for a unified field theory has been formulated: the Langrangian
must not decompose into irreducible parts, i.e., it must not be expressed as a sum of several
scalar densities but consist of a single “unified” term (cf. [308], p. 786). In principle, this was
accepted also by Einstein as reported in Section 7.1. Sciama’s unified field theory [567] forms an
example326.
A. Lichnerowicz called a theory “unitary in the strict sense”
-transformations, because these would mix the symmetric and
skew-symmetric parts of the connection and thus counter criticism of the type Pauli had phrased. A
further necessary condition for a unified field theory has been formulated: the Langrangian
must not decompose into irreducible parts, i.e., it must not be expressed as a sum of several
scalar densities but consist of a single “unified” term (cf. [308], p. 786). In principle, this was
accepted also by Einstein as reported in Section 7.1. Sciama’s unified field theory [567] forms an
example326.
A. Lichnerowicz called a theory “unitary in the strict sense”
“[…] if the exact field equations control an indecomposable hyper-field, and themselves
cannot be fractionized into propagation equations of the gravitational and of the electromagnetic
field but approximatively […].” ([371], p. 152)327
In Kaluza–Klein theory the gravitational and electromagnetic fields are encased in one and the same geometrical object, the 5-dimensional metric. Just one term in the Lagrangian is needed. By M.-A. Tonnelat, such a theory has been called “unified in a strong sense” [627, 641], p. XVII.328 In his thesis on a generalization of Kaluza–Klein theory, Y. Thiry had defined a unitary theory for two fields by the requirements (1) that the two fields emanate from the same geometry, and (2) that they amalgamate into one hyper-field of which they represent nothing more than two different aspects ([606], p. 13). An example for a hyper-field taken from history would be the electromagnetic field tensor within special relativity.
Bargmann’s second demand placed on UFT, the existence of stable solutions describing charged
particles, remained unfulfilled within the Einstein–Schrödinger theories. With singularities of the fields
being excluded, not even a satisfactory definition of a particle (beyond the concept of test particle)
could be given in such classical field theories. Einstein was very aware of this when he wrote to
Besso ([163*], p. 438): “E.g., a ‘particle’ in the strict sense of the word does not exist, because it
does not fit to the program of representing reality by everywhere continuous, even analytical
fields.”329 Even today, a convincing definition of an interacting particle apparently does not exist. We have free fields
describing particles and interaction terms introduced in the Lagrangian. Attempts at creating the concept of
a single particle including its interaction with other particles have been attempted, unsuccessfully, e.g., one
by G. Pétiau [494]. A precise definition of an interacting particle as a member of an ensemble of particles
seems not outdated, but out of reach.
Even today, a convincing definition of an interacting particle apparently does not exist. We have free fields
describing particles and interaction terms introduced in the Lagrangian. Attempts at creating the concept of
a single particle including its interaction with other particles have been attempted, unsuccessfully, e.g., one
by G. Pétiau [494]. A precise definition of an interacting particle as a member of an ensemble of particles
seems not outdated, but out of reach.
Methodological questions could be added. Why did Einstein, Schrödinger and most others working in unified field theory start with a metric and a connection as independent variables and then link them through a condition for the covariant derivative of the metric? To solve the latter condition for the connection has used up an immense amount of energy and time (plus printed paper) as we have seen before. Were they afraid of going one step back behind H. Weyl and other mathematicians who had recognized the independence of the concepts of metric and parallel transport? It might have been more direct to generalize, in a systematical investigation, the Levi-Civita connection (Christoffel symbol) by building the connection as a functional of the symmetric and skew-symmetric parts of the metric and their first derivatives as Hattori and Eisenhart have done.
19.1.2 UFT and quantum theory
Einstein’s position with regard to quantum mechanics, particularly his resistance to the statistical interpretation of it is well known, cf. [585, 586]. In this context, his abortive attempts at presenting contradictions within the Copenhagen interpretation of quantum mechanics during the 1927 Solvay conference in Brussels may be remembered. Ehrenfest’s remark there is quoted by Heisenberg: “I’ m ashamed of you, Einstein. You put yourself here just in the same position as your opponents in their futile attempts to refute your relativity theory” ([248], p. 107). A decade later, Einstein’s comment on Bohr’s riposte to the EPR-paper as reported by Léon Rosenfeld was that Bohr’s position was logically possible, but: “so very contrary to my scientific instinct that I cannot forego the search for a more complete conception.” ([518], p. 131).330 In his judgment on quantum mechanics, Einstein differed strongly from Pauli’s who believed in the completeness of quantum mechanics:
“This generalization of the concept ‘state’ which involves a strict renouncement of a
lawful description of the single, individual system for me seems to be necessary and, by
the way also understandable, in view of the facts mentioned earlier. It is a consequence
of the influence, unknown in principle, on the system being observed by the chosen
measuring device. Due to this state of affairs, only as a consequence of this renouncement
of a lawful description of an individual system seemingly is it possible to continue using
the conception of ‘closed system’ and the closely related notion of space and time.
In this sense, I deem the description of quantum mechanics to be complete.” ([489],
p. 520–521.)331
Therefore, Pauli questioned whether it was possible to unify the gravitational and electromagnetic fields in a classical field theory without taking note of “those facts in which the quantum of action plays an essential role”. In fact, already at the time suggestions for a “unitary” field theory in the framework of quantum (field) theory were made: E. Stueckelberg saw electron, proton, neutron and the then only neutrino as states of one more fundamental elementary particle; the unitary field is a spinor with 16 components [594]. This was a step further than the neutrino theory of light (cf. Section 1). Heisenberg’s later program of non-linear spinor theory as kind of a unified quantum field theory [247], although unsuccessful, belongs into this category. We are not surprised about Dirac’s opposition: In a letter to Heisenberg of 6 March, 1967 he wrote:
“My main objection to your work is that I do not think your basic (non-linear field) equation has sufficient mathematical beauty to be a fundamental equation of physics. The correct equation, when it is discovered, will probably involve some new kind of mathematics and will excite great interest among the pure mathematicians, just like Einstein’s theory of the gravitational field did (and still does). The existing mathematical formalism just seems to me inadequate.” (Quoted from [339*], p. 281.)
Perhaps, Dirac’s foible for linear equations was behind this judgment. Much earlier, in 1942, after a colloquium in Dublin in which Eddington and Dirac had taken part, Schrödinger complained to Max Born:
“Your idea of getting their opinion on Born’s theory is pathetic.332 That is a thing beyond their linear thoughts. All is linear, linear, – linear in the n’th power I would say if there was not a contradiction. Some great prophet may come …‘If everything were linear, nothing would influence nothing,’ said Einstein once to me.” ([446*], p. 272.)
In fact, quantum mechanics and quantum field theory live very much on linearity (Hilbert space, linear operators). In principle, this does not forbid quantization of non-linear classical field theories like the non-linear electrodynamics of Born and Infeld (cf. Section 5). Already in 1933, in connection with this non-linear electrodynamics, Max Born confronted Einstein’s opinion:
“For a long time Einstein had advocated the point of view that there must be a non-linear field theory containing the quantum laws. We have here a non-linear field theory, but I do not believe that the quantization can be dispensed with. […] I believe the following: every theory built up on classical foundations requires, for the completion of its assertions, an extension by initial and boundary conditions, satisfying only statistical laws. The quantum theory of the field provides this statistical completion […] through an inner fusion of the statistical and causal laws.” ([37], p. 434, 2nd footnote.)
Hence, Born’s attempts at a theory compatible with both gravitation and quantum theory definitely left the framework of UFT [39]. It seems that M.-A. Tonnelat accepted Born’s point of view.
A number of authors we have met before felt entitled to give general or very specific comments on
the relationship between UFT and quantum theory. J. Callaway came to the conclusion that:
“his [i.e., Einstein’s UFT] theory will either be able to handle quantum phenomena or it will
fail completely.” ([70], p. 780.) Moffat & Boal 1975 [443] just guessed: “It could be that the
main significance of the 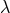 -gauge transformations lies in the fact that it may influence the
renormalizability of the theory. […]. It is possible that the unified field theory described here is
renormalizable, because of its invariance under the extended gauge group of transformations.” Within
Jordan–Thiry theory as a “strongly unified” theory in the sense of M.-A. Tonnelat, the idea
that its non-linearity would lead to elementary particles seemingly was given up. Moreover,
in Sections 4.2, 4.3 and 16.2 we encountered two attempts, both also unsuccessful, toward a
synthesis of classical field theory and quantum theory in the frameworks of wave geometry and
5-dimensional relativity. At the GR-2-Conference in Royaumont in 1959, Ph. Droz-Vincent
spoke about the quantization of the theory’s linear approximation; a mass term was introduced
by hand. The theory then was interpreted as “a unitary theory of graviton-photon” ([132],
p. 128).
-gauge transformations lies in the fact that it may influence the
renormalizability of the theory. […]. It is possible that the unified field theory described here is
renormalizable, because of its invariance under the extended gauge group of transformations.” Within
Jordan–Thiry theory as a “strongly unified” theory in the sense of M.-A. Tonnelat, the idea
that its non-linearity would lead to elementary particles seemingly was given up. Moreover,
in Sections 4.2, 4.3 and 16.2 we encountered two attempts, both also unsuccessful, toward a
synthesis of classical field theory and quantum theory in the frameworks of wave geometry and
5-dimensional relativity. At the GR-2-Conference in Royaumont in 1959, Ph. Droz-Vincent
spoke about the quantization of the theory’s linear approximation; a mass term was introduced
by hand. The theory then was interpreted as “a unitary theory of graviton-photon” ([132],
p. 128).
A desperate argument, from the point of view of physics, in favour of UFT was advanced at the same
conference by mathematician A. Lichnerowicz: there would be many good experiments in quantum theory,
but no good (quantum field) theories. In UFT at least, we would have a theory with a definite mathematical
meaning ([120*], p. 149). For some like A. Proca, the hope in Einstein’s genius overcame a sober assessment:
“Convinced that every ‘field’ could be subjected to a theory of the type he had developed, he [Einstein]
nurtured the ‘modest hope’ that such a theory possibly would bring forth the key to quantum theory.
[500]”333
In fact, Einstein’s claim that unified field theory would supersede quantum mechanics as a foundation for physics, could not be strenghtened by a recipe by which elementary particles were generated from classical field distributions. The concept of geon (“gravitational electromagnetic entity”) was introduced by J. A. Wheeler in 1955 [696] in order to form a classical model for an elementary particle. It turned out to be a tinkering with the global topology of solutions. Although approximate solutions of Einstein’s vacuum equations describing geons have been found (cf. [60]), they have not been proven to be stable entities. According to Wheeler
“A geon has exactly the property of being only an approximate solution; or rather, an accurate solution which is not fully stable with time – it leaks energy. Thus it is not in agreement with one’s preconceived idea that there should be a particle-like solution that is fully stable; but aren’t we being very brash if we say that the world isn’t built that way? […] Perhaps the stability of the particles we know is due to some intrinsic quantum character, which we cannot expect to show up before we have gone to the quantum level.” ([120*], p. 149)
Perhaps, this new concept led M.-A. Tonnelat once again to an optimistic comment ([635], p. 9):
“To the best of hypotheses, the unitary theories seem to explain, by classical methods, the
formation of corpuscular structures out of the unified field. This attribution of particles
to the field, postulated so energetically by Einstein, obviously is in a much too embryonic
state to naturally explain the existence of different types of elementary particles.” 334
Two years before, P. Bergmann’s programmatic statement at the Chapel Hill conference, i.e.,
“The original motivation of unified field theory is get a theory of elementary particles, which includes electrons and not only hyper-fragments, and furthermore obviate the need for quantization which would result from the intrinsic non-linearity”
had been instantly put into doubt by R. Feynman:
“Historically, when the unified field theory was first tackled, we had only gravitation, electrodynamics, and a few facts about quantization, […]. In the meantime, the rest of physics has developed, but still no attempt starts out looking for the quantum effects. There is no clue that a unified field theory will give quantum effects.” ([120], p. 149.)
Quantum mechanics, in particular as the measuring process is concerned, seemed not to have reached a generally accepted final interpretation. It looks as if Dirac wished to exploit this situation for making unitary field theory more respectable:
“And I think that it is quite likely that at some future time we may get an improved quantum mechanics in which there will be a return to determinism and which will, therefore, justify Einstein’s point of view.” ([126], p. 10.)
Dirac had in mind that application of the present quantum mechanics should not be pushed too far into domains of highest energy and smallest distances (p. 20). In view of the current brilliant empirical basis of quantum field theory, and the failure of all attempts to built a hidden-parameter theory, Dirac’s remark is far from supporting Einstein’s classical unified theory.
Einstein was well aware of the shortcomings of his “theory of the asymmetric field”. The last paragraph of Appendix II in the 5th Princeton edition of The Meaning of Relativity reads as:
“One can give good reasons why reality cannot at all be represented by a continuous field. From the quantum phenomena it appears to follow with certainty that a finite system of finite energy can be completely described by a finite set of numbers (quantum numbers). This does not seem to be in accordance with a continuum theory, and must lead to an attempt to find a purely algebraic theory for the description of reality. But nobody knows how to obtain the basis of such a theory” [158].
His remark in a letter of 10 August 1954 to M. Besso led into the same direction: “Yet, by all means, I consider
it as possible that physics cannot be founded on the field concept, i.e., on continuous structures. In this case, from
my whole castle in the air, gravitational theory included, but also from the rest of contemporary physics nothing
remains.”335
And, a fortnight before his death, he wrote that he did not want to dispense with “a complete real-description of the individual case” but also:
“On the other hand, it is to be admitted that the attempt to comprehend the undoubtedly
atomistic and quantum-structure of reality on the basis of a consequential field theory
encounters great challenges. By no means am I convinced that they can be overcome”336 ([159], p. XVI )
([159], p. XVI )
19.1.3 A glimpse of today’s status of unification
That unified field theory of the Einstein–Schrödinger type had become obsolete, was clear to theoretical physicists since the mid 1950s. In his introduction to the first conference on gravitation in Japan, in 1962, Nobel prize winner R. Utiyama wrote: “[…] it was no exaggeration to say that the old-fashioned mathematical investigation of Einstein’s theory was not regarded as a field of physics but rather a kind of mathematical play or a kind of metaphysics” ([662], p. 99). Einstein’s former assistant P. G. Bergmann was less harsh: “Einstein spent the last five years of his life investigating this theory (the ‘asymmetric’ theory) without arriving at clear-cut answers. At the present time, all unified field theories must be considered speculative. But for a scientist who believes in the intrinsic unity of the physical universe, this speculative inquiry has an irresistible attraction” ([22], p. 492).
The idea of unifying all fundamental physical interactions in one common representation is as alive
today as it was in Einstein’s times. Its concrete realizations differ from UFT in important points: quantum
fields are used, not classical ones, and all four fundamental interactions are taken into account – in
principle. At first, Grand Unified Theories (GUTs) unifying only the electromagnetic, weak, and strong
interactions were considered, e.g., with gauge group 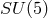 . The breaking of this symmetry to the
symmetry of the standard model of elementary particles
. The breaking of this symmetry to the
symmetry of the standard model of elementary particles 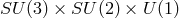 required the introduction
of Higgs fields belonging to unattractive large representations of
required the introduction
of Higgs fields belonging to unattractive large representations of 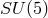 [561]. The concept of
“spontaneous symmetry breaking” implying a dynamics exhibiting the full symmetry and a
ground state with less symmetry is foreign to the Einstein–Schrödinger type of unitary theory.
The GUTs studied have made predictions on the occurrence of new particles at a mass-scale
(GUT-scale) outside the reach of present particle accelerators, and on the existence of topological
defects such as cosmic strings, or domain walls. None were detected up to now. There was also a
prediction on the decay of the proton by minimal
[561]. The concept of
“spontaneous symmetry breaking” implying a dynamics exhibiting the full symmetry and a
ground state with less symmetry is foreign to the Einstein–Schrödinger type of unitary theory.
The GUTs studied have made predictions on the occurrence of new particles at a mass-scale
(GUT-scale) outside the reach of present particle accelerators, and on the existence of topological
defects such as cosmic strings, or domain walls. None were detected up to now. There was also a
prediction on the decay of the proton by minimal 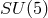 which remained unsupported by
subsequent measurements. Also, the simplest
which remained unsupported by
subsequent measurements. Also, the simplest 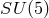 -GUT does not bring together in one point
the different energy-dependent couplings. This would be accomplished by a supersymmetric
-GUT does not bring together in one point
the different energy-dependent couplings. This would be accomplished by a supersymmetric
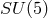 -GUT.
-GUT.
Apparently, a main purpose of string theory has been to consistently unify all gauge interactions with gravity. However, “string phenomenology”, i.e., the search for the standard model of elementary particles in (supersymmetric) string theory, has not been successful in the past 30 years. An optimistic assessment would be: “to obtain a connection between (string) theory and present (standard model) experiments is possible in principle but difficult in practice” ([451], p. 10).
The attempted inclusion of gravitation causes enormous conceptual and calculational difficulties which
have not yet been overcome by candidates for “Theories of Everything” (TOEs), as are superstring
theory,337
M-theory,338
brane-world scenarios339
etc. In the mid 1990s, the 5 existing superstring theories in time plus a 10-dimensional
space340
via dualities have been shown to reduce, effectively, to one remaining theory. The extra dimensions are a
means of allowing gravity to propagate into these dimensions while the other fundamental forces may be
confined to four-dimensional spacetime. Problems caused by the number of additional spacelike dimensions
required in modern unified theories are the unknown physics acting in them and the unacceptably large
number of possibilities for space-time: the extra dimensions can be compactified in a giant number of
different ways estimated to amount to 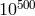 (string theory landscape). A way out has been claimed by
adherents of the multiverse-speculation: only a small number of the ground states are claimed to be
“habitable”. Thus, the fundamental constants of the universe would not be explained by physics but by
some form of the anthropic principle. Up to now superstring- or M-theory have not been able to make
explicit predictions about large distance physics. A recent presentation of string theory is given in
[14].
(string theory landscape). A way out has been claimed by
adherents of the multiverse-speculation: only a small number of the ground states are claimed to be
“habitable”. Thus, the fundamental constants of the universe would not be explained by physics but by
some form of the anthropic principle. Up to now superstring- or M-theory have not been able to make
explicit predictions about large distance physics. A recent presentation of string theory is given in
[14].
In contrast to UFT, the modern theory of unified fields in the form of a set of rules and hopes purported
by superstring theory has inspired greatly the development of some mathematical disciplines. Conceptually,
non-Abelian gauge theory, supersymmetry and their geometrical realizations, as well as the
renormalization group [461] now are part of the game. Even speculations about unification of such
different objects as are elementary particles, microscopic black holes, and string states have been
presented [522] – not to speak about even more speculative objects like black branes and blackfolds
[193].
It seems that today’s discussions divide theoretical physicists into two groups: those striving for a “Theory of Everything”341 as the modern equivalent to UFT, and those believing that this is the kind of reductionism already disproved by present physical theory, in particular by many-particle-phenomena [350]. In one of today’s approaches, conceptual unification, i.e., the joinder of Heisenberg’s uncertainty relations to gravitational theory (general relativity) and grand unification, has been set apart from the unification of spin-2-particles with all the other (elementary) particles, cf. [521].342 The second point listed above could be expressed in more generality as: “One of the main goals of unified theory should be to explain the existence and calculate the properties of matter” ([236], p. 288). True, the present designs of TOEs have absorbed an immense amount of knowledge gained, theoretically and empirically, since the old days of classical UFT. Nevertheless, the elementary particle mass-spectrum is as unexplained today as it was then. In spite of the lauded Higgs-mechanism, the physical origin of mass is far from being understood. There seems to be a sizeable number of physicists with reserved attitude toward modern unified field theories.
19.2 Observations on psychological and philosophical positions
19.2.1 A psychological background to UFT?
According to guesswork propagated in the community, one of the reasons why both Albert Einstein
and Erwin Schrödinger engaged in their enduring search for a unified field theory was that
they hoped to repeat their grand successes: general relativity and its positive empirical test
in 1919, and wave mechanics with its quick acceptance, in 1926. Schrödinger wrote to one
of his lady lovers in January 1947 that he “had completely abandoned all hope of ever again
making a really important contribution to science.” But now, it looked as if he had been sent
to Ireland by “the Old Gentleman” to live freely, without direct obligations, and follow his
fancies. Which, of course, had brought him to the present final solution of how to set up unified
field theory. His biographer W. Moore claimed that Schrödinger “was even thinking of the
possibility of receiving a second Nobel prize” ([446] p. 434). In a way, world fame seems to cause
addiction.
With Einstein, matters were more complicated. He certainly had no such wishes as Schrödinger; instead, he enjoyed using his fame as a propellant for making known his views, in other fields than in physics, in public.343 But, why would he begin anew with mixed geometry after roughly two decades? Did he want to not leave the territory to Schrödinger who had wandered into it since 1943 and had believed to be able to do better than Einstein? Einstein did not strive for a second Nobel prize, but was tied up by his philosophical thinking about reality and causality. It led him to believe that the epistemological basis of the ideas that had once lead to a splendid result, the geometrization of the gravitational field within the framework of the continuum, by necessity must work again.
“The gravitational equations could be found only due to a purely formal principle (general
covariance), i.e., due to faith in the imaginably greatest logical simplicity of the laws of
nature. Because it was evident that the theory of gravitation was but a first step toward
the discovery of field laws, it appeared to me that this logical way first must be thought to
its end; only then one can hope to arrive at a solution to the quantum problem.” Einstein
to de Broglie 8 February 1954 ([580], Appendix A.2.8.)344
In the same letter, Einstein explained why he did not want to look like an “[…] ostrich
permanently hiding his head in the relativistic sand in order to not have to face up to the evil
quanta.”345 He thought this explanation could interest de Broglie “from a psychological point of view, […].”
He thought this explanation could interest de Broglie “from a psychological point of view, […].”
That successful physicists tend to come back to fruitful ideas in their previous work can be seen also in W. Heisenberg. In his case, the idea was to build theories just containing observables. His introduction of the S-matrix followed this objective he had applied when making the transition to quantum mechanics. Although valuable for scattering probabilities, and followed and extended by a number of well-known theoreticians, it has been criticized as having held up progress in elementary particle physics (Yang–Mills theory) [423].
At the very end of his life, Einstein was disappointed; he blamed “the physicists proper” for not understanding progress made by him. This is shown by his letter to Hans Mühsam of February 22, 1955:
“However, recently I decisively made progress. It refers to an improvement of the theory
as far as its structure is concerned, but not with regard to finding solutions which could
be examined through the [empirical] facts. […] The matter is very plausible in itself and
as perfect as to find increased interest among mathematicians. The physicists proper are
rejecting it because they happened to maneuver themselves into a dead end – without
noticing.” 346
The reference to “the mathematicians” leads us back to Einstein’s “logical-philosophical” thinking
(letter to M. Solovine, 12 February 1951) in his later years as compared to physical argumentation.
Fortunately, Einstein did not live long enough to be confronted with the deadly blow by Wyman &
Zassenhaus (Section 9.6.2) to his idea that knowledge of regular exact solutions would bring an
advancement in the understanding of UFT.
From a point of view from outside the UFT-community, M. Fierz assessed the whole endeavor. In a
letter to Pauli of October 9, 1951 he compared UFT with a particular tendency in psychology:
“Likewise, the field-concept is analogous to the idea of milieu. Today, group-psychology is a big
fashion in England and America. It is somewhat like Einstein’s unitary field theory in the sense
that the collective milieu is to explain everything such as the general field is to contain the
whole of physics. Human beings are thus downgraded to herd animals – are made mechanical
[…].”347 ([490], p. 382.) His comparison seems to be a bit far-fetched, though. Perhaps, he felt that the field concept
was no sufficient substitute for the notion of particle.
([490], p. 382.) His comparison seems to be a bit far-fetched, though. Perhaps, he felt that the field concept
was no sufficient substitute for the notion of particle.
S. Schweber found a parallel between the manner of Einstein’s theorizing and his views regarding world government and the organization to be established for preventing war ([563], p. 96).
19.2.2 Philosophical background
Often, mathematicians tend to be attracted by Platonic philosophy which assumes the existence of a world of ideas characterized by concepts like truth and beauty – with the possibility of only an approximative empirical approach to it. As H. Kragh pointed out in his biography of Dirac, since the 1930s Dirac supported the claim that, by following mathematical beauty, important advances in theory can be made ([339*], p. 282). Kragh distinguished two aspects as to the function of such a “principle of mathematical beauty”: it may serve as a recommendation for the process of theory-building, but it also may be used for a justification of a theory without strong empirical footing. In his Spencer Lecture of 1933, Einstein did not content himself with mathematical beauty:
“I am convinced that we can discover by means of purely mathematical constructions
the concepts and the laws connecting them with each other, which furnish the key
to the understanding of natural phenomena. Experience may suggest the appropriate
mathematical concepts, but they most certainly cannot be deduced from it. Experience
remains, of course, the sole criterion of physical utility of a mathematical construction.
But the creative principle resides in mathematics. In a certain sense, therefore, I hold it
true that pure thought can grasp reality, as the ancients dreamed.”348
Pauli found astonishing “[…] Einstein’s habit to call all those content with
quantum mechanics ‘positivists’, ‘empiricists’, ‘sensualists’, ‘phenomenalists’, or the
like.”349 In a personal note by him, we can read: “According to Einstein, proponents of quantum mechanics should
say: ‘the description is incomplete, yet its completion is meaningless because it has nothing to do with
laws of nature.’ Reduces to the question whether something about which no knowledge can be
obtained exists. Einstein comments his own field theory ‘these laws are in Heaven, but not on
Earth.”350
In a personal note by him, we can read: “According to Einstein, proponents of quantum mechanics should
say: ‘the description is incomplete, yet its completion is meaningless because it has nothing to do with
laws of nature.’ Reduces to the question whether something about which no knowledge can be
obtained exists. Einstein comments his own field theory ‘these laws are in Heaven, but not on
Earth.”350 cf. ([491*], 11 April 1953, p. 110).
cf. ([491*], 11 April 1953, p. 110).
After having worked on unified field theory since 1925, and having moved farther and farther away from
experimental or observational evidence, Einstein needed such an epistemological and methodical
justification for his research. He was convinced that there “is no logical path leading from the empirical
material to the general principle which then supports logical deduction. […] The further theory progresses,
the clearer it becomes that the fundamental laws cannot be found inductively from the empirical facts (e.g.,
the gravitational field equations or the Schrödinger equation of quantum mechanics).” ([163*],
p. 468.)351 Also, while Einstein ascribed a “creative principle” to mathematics, he just used this discipline as a quarry
for the building of physical theories. After his decision for mixed geometry, a further creative influence of
mathematics on his work can hardly be found. A mathematician who had followed the work in UFT by
Einstein and others until 1945, stated bluntly:
Also, while Einstein ascribed a “creative principle” to mathematics, he just used this discipline as a quarry
for the building of physical theories. After his decision for mixed geometry, a further creative influence of
mathematics on his work can hardly be found. A mathematician who had followed the work in UFT by
Einstein and others until 1945, stated bluntly:
“[…] the failure up to 1945 of the attempts at a unified theory might have been anticipated: each attempt was geometry and nothing more. The truism that, to get something empirically verifiable out of mathematics, something empirically known must be put into mathematics, appeared to have been overlooked” [18].
Now, many years later, we are permitted to extend Bell’s date past 1945 until the end of the 1960s.
What is reality?
A central matter of dispute was Einstein’s conception of reality. Philosophers of science have defined different categories of realism; to give as an example the one underlying the EPR-paper. Einstein’s position then is classified accordingly; cf. [197], its review [62], and an interpretation of Einstein’s understanding of locality and separability [289]. The following lines just reflect some aspects which have come up during this review.
W. Pauli formulated his opinion on the difference between Einstein and quantum physicists in a letter of
29 June 1953 to the Austrian philosopher F. Kröner (1989 – 1958): “It is due to the Einstein’s restrictive
philosophy’ whereby an ‘objective description of nature’ is only such a description which demands
potential validness without explicit reference to observation** (‘detached observers’).” ([491*],
p. 184–185.)352 The annotation** reads as: “cf. also the final sentence of Einstein’s ‘The Meaning of Relativity’,
4. Ed. 1953, Princeton University Press.” The last two sentences in [156] have been quoted
already toward the end of Section 9.3. In a letter to Heisenberg of 5 Juli 1954, Pauli explicated
this:
The annotation** reads as: “cf. also the final sentence of Einstein’s ‘The Meaning of Relativity’,
4. Ed. 1953, Princeton University Press.” The last two sentences in [156] have been quoted
already toward the end of Section 9.3. In a letter to Heisenberg of 5 Juli 1954, Pauli explicated
this:
“Essentially Einstein begins with a ‘realistic metaphysics’ (NB not with a deterministic
one) assuring him a priori that observation cannot generate a state; e.g., if an observation
leads to a (‘quasi-sharp’) position, then, in the ‘objective-realistic description’ of nature,
even before the observation an ‘element’ would have been there which somehow ‘corresponds’
to the result of the observation. From it, Einstein infers his realistic dogma that in
the ‘objective-realistic description’ the position of an electron ought to be determined
‘quasi-sharply’ always (in all states), i.e., up to quantities of ca. 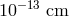 . Likewise,
the position of the moon is determined independently of how we look at it. […] The
background of Einstein’s realistic metaphysics is formed by his belief that only it can
ensure differentiation between the ‘real’ and what is merely imagined (dream, hallucination).”
([491*], p. 706–707.)353
. Likewise,
the position of the moon is determined independently of how we look at it. […] The
background of Einstein’s realistic metaphysics is formed by his belief that only it can
ensure differentiation between the ‘real’ and what is merely imagined (dream, hallucination).”
([491*], p. 706–707.)353
In the same direction went Pauli’s letter to Max Born of 3 March 1954:
In conversations with Einstein, I have now seen that he takes exception to the essential
premise of quantum mechanics that the “state” of a system is defined only by the specification
of an experimental arrangement.[…] Einstein absolutely does not want to accept this. If
one could measure precisely enough, this would be as true for macroscopic beadlets as
for electrons. […] But Einstein keeps the “philosophical” prejudice that (for macroscopic
bodies) under all circumstances a “state” (said to be “real”) can be “objectively” defined.
This means without assigning an experimental set-up with the help of which the system
(of macroscopic bodies) is investigated […]. It appears to me that the discrepancy with
Einstein may be reduced to this (his) assumption which I have called the notion or the
“ideal” of the “detached observer”.354 ([491], p. 509–510.)
([491], p. 509–510.)
In fact, for Einstein the quantum mechanical state function 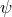 could not be interpreted as a
“Realzustand”: “The Realzustand cannot at all be described in present quantum theory but only
(incomplete) knowledge with regard to a Realzustand. The ‘orthodox’ quantum theorists ban the concept of
Realzustand in the first place (due to positivist considerations)”. Einstein to Besso 10 August 1952 ([163],
p. 483).355
could not be interpreted as a
“Realzustand”: “The Realzustand cannot at all be described in present quantum theory but only
(incomplete) knowledge with regard to a Realzustand. The ‘orthodox’ quantum theorists ban the concept of
Realzustand in the first place (due to positivist considerations)”. Einstein to Besso 10 August 1952 ([163],
p. 483).355 This dispute might also be taken as an example for debaters using different categories: with Einstein
arguing from ontology and Pauli methodologically. Modern experiments have vindicated Pauli’s judgement
about quantum physics and made obvious “the failure of Einstein’s attempt to show the incompleteness of
quantum theory.” ([459], p. 182)
This dispute might also be taken as an example for debaters using different categories: with Einstein
arguing from ontology and Pauli methodologically. Modern experiments have vindicated Pauli’s judgement
about quantum physics and made obvious “the failure of Einstein’s attempt to show the incompleteness of
quantum theory.” ([459], p. 182)
Until his death, Einstein insisted upon describing reality by a continuous field theory. In a letter of 16 October 1957 to Fierz, Pauli traced Einstein’s attitude to an ancient philosophical dispute:
“I do not doubt that classical field physics pretty directly originates from the Stoa,
in a continuous trend passing the ideas of the Renaissance and of the 17th century
[…]. Insofar the synthesis of quantum theory and general relativity (and, generally, field
quantization) is an unsolved problem, the old (ancient) conflict between atomists and the
stoics continues.”356 ([493], p. 571)
([493], p. 571)