14 Additional Contributions from Japan
We already met Japanese theoreticians with their contributions to non-local field theory in Section 3.3.2, to wave geometry as presented in Section 4.3, and to many exact solutions in Section 9.6.1. The unfortunate T. Hosokawa showed, in the paper mentioned in Section 4.3, that “a group of motions of a Finsler space has at most 10 parameters” [287]. Related to the discussion about exact solutions is a paper by M. Ikeda on boundary conditions [299]. He took up Wyman’s discussion of boundary conditions at spacelike infinity and tried to formulate such conditions covariantly. Thus, both spacelike infinity and the approach to it were to be defined properly. He expressed the (asymmetric) metric by referring it to an orthormal tetrad tetrad , where
, where  are the tetrad vectors,
orthonormalized with regard to
are the tetrad vectors,
orthonormalized with regard to 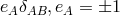 . The boundary condition then was
. The boundary condition then was 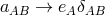 for
for
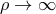 , where
, where 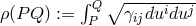 and the integral is taken over a path from
and the integral is taken over a path from 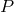 to
to  on a spacelike hypersurface
on a spacelike hypersurface 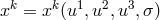 with parameters
with parameters 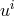 and metric
and metric
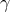 .
.
Much of the further research in UFT from Japan to be discussed, is concerned with structural
features of the theory. For example, S. Abe and M. Ikeda generalized the concept of motions
expressed by Killing’s equations to a non-symmetric fundamental metric [1]. Although the Killing
equations (43*) remain formally the same, for the irreducible parts of 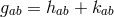 , they read as:
, they read as:
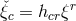 . All index-movements are done with
. All index-movements are done with 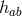 . The authors derive integrability
conditions for (497*); it turns out that for space-time the maximal group of motions is a 6-parameter
group.267
. The authors derive integrability
conditions for (497*); it turns out that for space-time the maximal group of motions is a 6-parameter
group.267
Possibly, in order to prepare a shorter way for solving (30*), S. Abe and M. Ikeda engaged in a
systematic study of the concomitants of a non-symmetric tensor 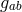 , i.e., tensors which are functionals of
, i.e., tensors which are functionals of
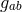 [301*, 300]. A not unexpected result are theorems 7 and 10 in ([301], p. 66) showing that any
concomitant which is a tensor of valence 2 can be expressed by
[301*, 300]. A not unexpected result are theorems 7 and 10 in ([301], p. 66) showing that any
concomitant which is a tensor of valence 2 can be expressed by 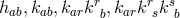 and scalar
functions of
and scalar
functions of 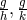 as factors. In the second paper, pseudo-tensors (e.g., tensor densities) are
considered.
as factors. In the second paper, pseudo-tensors (e.g., tensor densities) are
considered.
A different mathematical interpretation of Hoffmann’s meson field theory as a “unitary field theory” in the framework of what he called “sphere-geometry” was given by T. Takasu [598]. It is based on the re-interpretation of space-time as a 3-dimensional Laguerre geometry. The line element is re-written in the form
It can be viewed as “the common tangential segment of the oriented sphere with center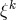 and radius
and radius
![r = ∫ [ϕsxk )dξs+ ϕ4 (xk )]dt dt](article2720x.gif) …” ([599].
…” ([599].