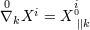 introduced in
(14*) by shifting the number
introduced in
(14*) by shifting the number  from the index
from the index 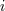 , i.e.,
, i.e., 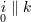 , to the sign of the derivation, i.e.,
, to the sign of the derivation, i.e.,  . This simplifies
notation, in particular if the same covariant derivative is applied to all indices of a tensor:
. This simplifies
notation, in particular if the same covariant derivative is applied to all indices of a tensor: 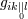 in place of
in place of
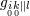 .
.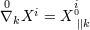 introduced in
(14*) by shifting the number
introduced in
(14*) by shifting the number  from the index
from the index 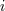 , i.e.,
, i.e., 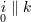 , to the sign of the derivation, i.e.,
, to the sign of the derivation, i.e.,  . This simplifies
notation, in particular if the same covariant derivative is applied to all indices of a tensor:
. This simplifies
notation, in particular if the same covariant derivative is applied to all indices of a tensor: 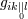 in place of
in place of
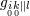 .
.