Note, that the 2nd term in Thirring’s expression (514) is also contained in (516) due to Tonnelat’s different notation. In
another paper, even 4 free parameters were used: the first term in (516) obtained a free parameter of its own. Cf. [413*]. All of
Thirring’s terms are contained in a Lagrangian given by S. Lederer and decorated by her with free parameters 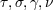 ([354*], Eq. (III.23) p. 256). After the Lagrangian (516) is multiplied by 2 and compared with Lederer’s, then her parameters
([354*], Eq. (III.23) p. 256). After the Lagrangian (516) is multiplied by 2 and compared with Lederer’s, then her parameters
 correspond to
correspond to  , respectively.
, respectively.
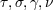 ([354*], Eq. (III.23) p. 256). After the Lagrangian (516*) is multiplied by 2 and compared with Lederer’s, then her parameters
([354*], Eq. (III.23) p. 256). After the Lagrangian (516*) is multiplied by 2 and compared with Lederer’s, then her parameters
 correspond to
correspond to  , respectively.
, respectively.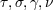 ([354*], Eq. (III.23) p. 256). After the Lagrangian (516*) is multiplied by 2 and compared with Lederer’s, then her parameters
([354*], Eq. (III.23) p. 256). After the Lagrangian (516*) is multiplied by 2 and compared with Lederer’s, then her parameters
 correspond to
correspond to  , respectively.
, respectively.